Molecular Information Theory:
From Clinical Applications To Molecular Machine Efficiency
Dr. Thomas D. Schneider
ABSTRACT
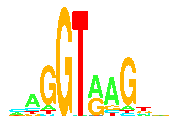 Information theory was introduced by Claude Shannon in 1948 to precisely
characterize data flows in communications systems. The same mathematics can
also be fruitfully applied to molecular biology problems. We start with the
problem of understanding how proteins interact with DNA at specific sequences
called binding sites. Information theory allows us to make an average
picture of the binding sites and this can be shown with a computer graphic
called a
sequence logo
(https://alum.mit.edu/www/toms/glossary.html#sequence_logo).
Information theory was introduced by Claude Shannon in 1948 to precisely
characterize data flows in communications systems. The same mathematics can
also be fruitfully applied to molecular biology problems. We start with the
problem of understanding how proteins interact with DNA at specific sequences
called binding sites. Information theory allows us to make an average
picture of the binding sites and this can be shown with a computer graphic
called a
sequence logo
(https://alum.mit.edu/www/toms/glossary.html#sequence_logo).
 Sequence logos show how strongly parts of a binding site are conserved,
in bits of information. They have been used to study a variety of
genetic control systems. More recently the same mathematics has been used to
look at individual binding sites using another computer graphic called a
sequence walker
(https://alum.mit.edu/www/toms/glossary.html#sequence_walker).
Sequence walkers are being used to predict whether changes
in human genes cause mutations or are neutral polymorphisms. It may be
possible to predict the degree of colon cancer by this method.
Sequence logos show how strongly parts of a binding site are conserved,
in bits of information. They have been used to study a variety of
genetic control systems. More recently the same mathematics has been used to
look at individual binding sites using another computer graphic called a
sequence walker
(https://alum.mit.edu/www/toms/glossary.html#sequence_walker).
Sequence walkers are being used to predict whether changes
in human genes cause mutations or are neutral polymorphisms. It may be
possible to predict the degree of colon cancer by this method.
 Information theory can also be used to understand the relationship between
the binding energy dissipated when two molecules stick together and the
amount of sequence conservation of the molecules measured in bits. Using the
Second Law of Thermodynamics, this relationship can be expressed as the
efficiency of the molecular interaction. Surprisingly, many molecular
systems including genetic systems, visual pigments and motility proteins have
efficiencies near 70%. A purely geometrical explanation of this result shows
that although biological systems are selected to have the highest efficiency,
it is restricted to 70% because having precisely distinguishable molecular
states is more important.
Information theory can also be used to understand the relationship between
the binding energy dissipated when two molecules stick together and the
amount of sequence conservation of the molecules measured in bits. Using the
Second Law of Thermodynamics, this relationship can be expressed as the
efficiency of the molecular interaction. Surprisingly, many molecular
systems including genetic systems, visual pigments and motility proteins have
efficiencies near 70%. A purely geometrical explanation of this result shows
that although biological systems are selected to have the highest efficiency,
it is restricted to 70% because having precisely distinguishable molecular
states is more important.


Schneider Lab
origin: 2003 July 15
updated: 2006 July 07

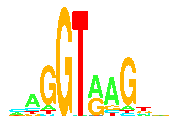 Information theory was introduced by Claude Shannon in 1948 to precisely
characterize data flows in communications systems. The same mathematics can
also be fruitfully applied to molecular biology problems. We start with the
problem of understanding how proteins interact with DNA at specific sequences
called binding sites. Information theory allows us to make an average
picture of the binding sites and this can be shown with a computer graphic
called a
sequence logo
(https://alum.mit.edu/www/toms/glossary.html#sequence_logo).
Information theory was introduced by Claude Shannon in 1948 to precisely
characterize data flows in communications systems. The same mathematics can
also be fruitfully applied to molecular biology problems. We start with the
problem of understanding how proteins interact with DNA at specific sequences
called binding sites. Information theory allows us to make an average
picture of the binding sites and this can be shown with a computer graphic
called a
sequence logo
(https://alum.mit.edu/www/toms/glossary.html#sequence_logo).