 Thomas Schneider received his Ph.D. from the University of Colorado, Boulder
in 1984. He continued the same project, on molecular information theory,
in both his postdoctoral work and at
Thomas Schneider received his Ph.D. from the University of Colorado, Boulder
in 1984. He continued the same project, on molecular information theory,
in both his postdoctoral work and at
 Thomas Schneider received his Ph.D. from the University of Colorado, Boulder
in 1984. He continued the same project, on molecular information theory,
in both his postdoctoral work and at
Thomas Schneider received his Ph.D. from the University of Colorado, Boulder
in 1984. He continued the same project, on molecular information theory,
in both his postdoctoral work and at
If you want to understand life, don't think about vibrant, throbbing gels and oozes, think about information technology. --- Richard Dawkins, The Blind Watchmaker, 1986.
I believe that living things are so beautiful that there must be a mathematics that describes them. In 1978, in the lab of Larry Gold in Boulder, Colorado, I started looking for mathematical ways to describe ribosome binding sites. I was working with frequency tables of the bases in the sites and gave a talk to some computer scientists. After the presentation Andrzej Ehrenfeucht, the head of the group, suggested, "Why don't you try the information transform?" I asked, "What's that?" He wrote "p log p" on the blackboard. I asked, "What does that mean?" "Oh, you go look it up!"
Half a year later I got around to computing the information, and got 11.0 bits. But what did that mean? I soon realized that I could also compute how much information would be needed to find the binding sites, given the size of the genome and number of binding sites. I was stunned to get 10.6 bits. I was able to confirm for other genetic systems that the sequence conservation at binding sites (Rsequence, measured in bits) is close to the information needed to find them (Rfrequency, also in bits). That discovery launched my career.
At first, describing ribosomal processes in terms of information may seem simple. After all, it's trivial to compute the expected frequency of EcoRI sites (5' GAATTC 3') as one in 4096 random bases. However, for ribosomes, the size of the genome and number of genes are fixed by physiology and history but the patterns at the sites could be anything.
Indeed, I soon discovered that the region around bacteriophage T7 promoters has 35.4 bits but only 16.5 bits are needed to find them. Either the budding theory---that binding site conservation evolves to match the minimum information needed to find the sites in the genome---was wrong or the data were telling us something new. I set out to do experimental work on these promoters. After four years of attempting to select for functional promoters, I found out that a functional T7 promoter will kill cells within 3 minutes of induction. To get around this problem, I used a toothpicking screen to isolate functional promoters from a chemically synthesized random library of T7 promoter variants. The variations destroyed the excess information and I found that the polymerase only needs 18 +/- 2 bits to be strong enough to kill cells. Presumably the excess information represents the binding sites of another protein; we are now hunting for it in the lab.
Information theory has been extremely fruitful for describing binding sites in more than 50 genetic systems. At my web site, https://alum.mit.edu/www/toms/, you will see two kinds of pretty graphics: sequence logos and sequence walkers. I invented sequence logos with my first Werner H. Kirsten Student Intern Program high school student, Mike Stephens. Using information to measure the sequence conservation at each position across a binding site, they represent an average picture of a collection of binding sites. They replace consensus sequences for making a picture of what sites look like and can show which face of the DNA a protein binds to. The area under a logo is Rsequence.
Logos give only an average picture. Can we assign an information content value to each individual binding site sequence so that their average is Rsequence? Marvelously, the mathematics "melts in your mind" to give a simple formula. My friend John Spouge (NCBI, NLM) then proved that this is the only possible formula that satisfies the averaging criterion.
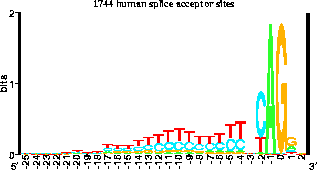 My friend Pete Rogan (ABL, now at Children's Mercy Hospital, Missouri)
found a paper claiming that a certain T to C
change at a splice junction in hMSH2 caused colon cancer.
Pete looked at our splice acceptor logo
(see figure)
and realized that nearly
50% of the time there are Cs there.
The people working on hMSH2 had forgotten the original
data when they made their consensus sequence!
Bert Vogelstein showed that 2 of 20 normal people have the change,
so it is indeed a polymorphism.
This case convinced us that information theory would be useful
in predicting splicing effects in key disease genes.
My friend Pete Rogan (ABL, now at Children's Mercy Hospital, Missouri)
found a paper claiming that a certain T to C
change at a splice junction in hMSH2 caused colon cancer.
Pete looked at our splice acceptor logo
(see figure)
and realized that nearly
50% of the time there are Cs there.
The people working on hMSH2 had forgotten the original
data when they made their consensus sequence!
Bert Vogelstein showed that 2 of 20 normal people have the change,
so it is indeed a polymorphism.
This case convinced us that information theory would be useful
in predicting splicing effects in key disease genes.
To show how splice junction changes affect the individual information content, I invented a computer graphic that `walks' across a sequence at one's command. With these sequence walkers, complicated splice junction mutations can be understood in seconds. One of my favorite cases is a low information content cryptic site lurking next to a strong normal site that is sitting on the end of an exon. A mutation of the sequence drops the information content of the site while simultaneously (!) raising the information content of the cryptic, which takes over. Since the cryptic site is out of frame, the protein is destroyed. We have analyzed more than 100 human splice junction mutations using information theory. Jim Ellis (OD/ORS/OD/BEPSP) has recently joined us. He is handling several international collaborations and is also set up on the main campus to do these analyses for scientists at NIH [see box].
|
Jim Ellis (OD/ORS/BEPSP, ellisj@ors.od.nih.gov, 301-496-4472, fax: 301-496-6608, Bldg 13, Rm 3W-16A) has set up Tom Schneider's Delila programs to do splice junction analyses for scientists at NIH. Published or unpublished sequence data can be used but it is most efficient to start with GenBank flat file format. Dr. Ellis can begin the analysis if he has a GenBank accession number (or the sequence) and the sequence changes on a floppy disk or by email. See https://alum.mit.edu/www/toms/spliceanalysis.html for further information. |
In 1983, I set out to understand how the information values I was measuring are related to the binding energy. The data were indicating a proportionality. What did that mean? Claude Shannon, who developed information theory 50 years ago, not only gave us a way to measure the amount of information, but also a way to determine how much information can be sent through a communications channel. This `channel capacity' is determined by the thermal noise and the energy dissipated. It can be used to find the maximum information that can be gained for a given energy dissipation. Surprisingly, I found that this is a new version of the Second Law of Thermodynamics. Using this I was able to convert my proportionality to an efficiency of 70%. This means that 30% of the binding energy is `wasted' because it is dissipated but does not contribute to the choices being made. Why? The mystery deepened when I stumbled on the fact that the quantum efficiency of rhodopsin is also 70%. That is, for every 100 photons that are absorbed and that excite a rhodopsin molecule, only in 70 cases does the rhodopsin change states. Later, at a lecture on muscle, I guessed that muscular efficiency would be the same, and was surprised to find that it is.
I went deeper into the theory and in 1989 found an elegant, purely geometric answer that explains why so many molecular machines are 70% efficient. I've been trying to finish the publications ever since then!
Where will this lead us? Information theory has proven itself in hundreds of genetic systems and the door is now open for understanding any molecular interaction or state change using these well developed mathematical tools. In particular, I think the key to the future is coding theory. Fortunately communications engineers have not been idle for the last 50 years. Telephone clarity, crisp CD music and reliable internet protocols are all based on the error correcting codes predicted by Shannon. We are now in the same position in biology: there must be codes for molecular interactions; we only need to find them. Sequence logos and walkers appear to be a good start.
Knowledge of information theory in biological systems can enlighten molecular design and provide a theoretical grounding for nanotechnology. In my lab, the theory has led to our inventing a practical molecular computer which is patent pending. Three other patentable nanotechnology projects are also in the works.
![]()

Schneider Lab
origin: 1999 May 4
updated: version = 1.16 of nihcatalyst.html 2002 May 27
![]()