In the original ev model of information gain in biological systems, when two organisms in competition had the same number of mistakes---a tie---both were allowed to survive. William A. Dembski claimed that this rule introduces information into the genomes of the organisms. The claim was tested by removing the rule either by randomly killing one of the competitors or by relying on the arbitrary internal details of the quicksort sorting algorithm. In both cases the information content of the sites still increased to the theoretically predicted value, disproving Dembski's claim.*
William A. Dembski claims that the ev program does not demonstrate an information increase because of the SPECIAL RULE. His claim is:
For instance, in the crucial paragraph from his article that I quoted above, Schneider remarks parenthetically: "To preserve diversity [of organisms], no replacement takes place if [the number of mistakes is] equal." Schneider's Pascal source code reveals why: "SPECIAL RULE: if the bugs have the same number of mistakes, reproduction (by replacement) does not take place. This ensures that the quicksort algorithm does not affect who takes over the population. [1988 October 26] Without this, the population quickly is taken over and evolution is extremely slow!" (9) Schneider is here fine-tuning his evolutionary algorithm to obtain the results he wants. All such fine-tuning amounts to investigator interference smuggling in complex specified information.
The SPECIAL RULE deals with the case in which two organisms have the same number of mistakes. The SPECIAL RULE is that when the mistakes are equal, neither organism is eliminated during the reproduction step. (Normally, with unequal mistakes, one organism replicates and takes over the spot of the other, thereby killing it.) I implemented this rule because otherwise one organism may have an arbitrary advantage coming from where it happens to be placed by the sorting algorithm. Since I thought that that is unnatural and biased, it was better to put the rule in place. At the time I found that the rule decreased the speed of the evolution.
In nature ties during competition can have any result. Two animals may back off (which represents the SPECIAL RULE), or they may duel to the death, with one winning by luck. So either method would be reasonable. Allowing the sorting algorithm to decide is somewhat akin to allowing the animal that happens to be higher on the side of a cliff to win when they are otherwise equivalent, so (contrary to my original thinking) this is also a reasonable scenario.
Dembski's claim is that the SPECIAL RULE (i.e. backing off) introduces information into the system and that this accounts for the information increase.
This claim was easily tested by modifying the program to remove or alter the SPECIAL RULE.
The ev program was modified from version 3.67 to version 3.69 so that there is a new parameter that allows one to select between the three possible methods for handling ties. The program will automatically upgrade older versions of the parameter file (evp) by adding this parameter.
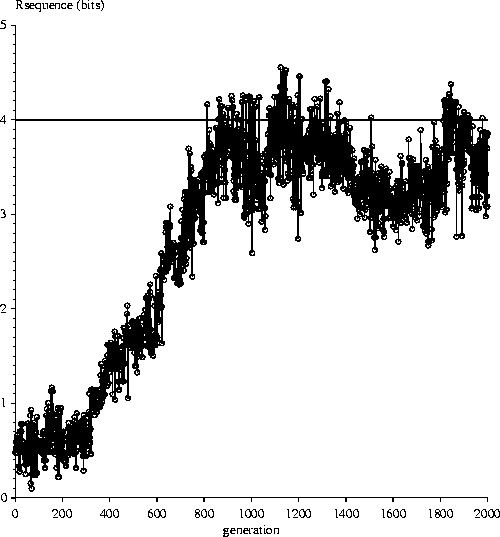
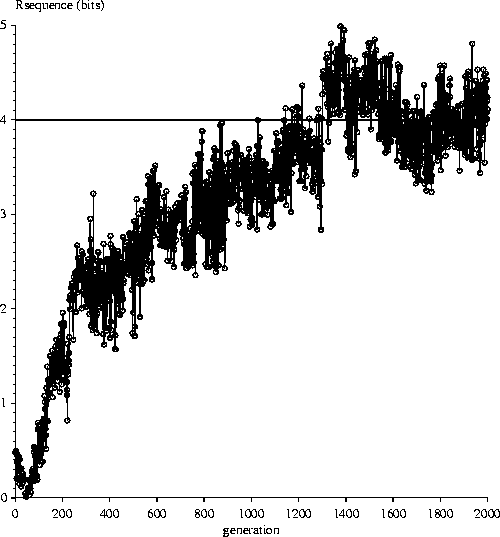
Except for the SPECIAL RULE, the program parameters were chosen to be the same as in the original paper with genome size G = 256 and number of sites gamma = 16 so the Rfrequency is log2256/16 = 4 bits/binding site. Below are the results for evolutions under the three different conditions for how to handle the situation when two organisms are tied by having the same number of mistakes.
For the condition where both organisms survive a tie, the ev program still produces the same graph as previously published, given the same parameters, demonstrating that the code was not significantly altered.
All three methods of handling a tie show an increase in the information content of the binding sites. In each case the information content increases from 0 bits to about 4 bits, as predicted by theory. Therefore William A. Dembski's claim, that backing off from a tied contest introduces information into the ev model, is incorrect.
Surprisingly, with a different initial parameter file (data not shown, substitute r, b or s for zzz to use it), the sorting algorithm produced faster evolution than the other two methods, opposite to what Dembski would have claimed. Why is evolution faster with the sorting algorithm in that case? This is not clear, but it is likely that it is the luck of the draw. Some initial conditions speed up and others may slow down the evolution.
I thank Douglas Theobald for alerting me to Dembski's posting and Ilya Lyakhov for useful comments.
(* Note: a rebuttal of Dembski's other statements is given on another page.)
Schneider Lab
origin: 2001 June 6
updated: version = 2.11 of claimtest.html 2016 Feb 29
(The blank lines above allow the
note
to be seen
if one jumps to it from the top of the page.)