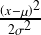Mathematical Terms of Biological Information Theory
version = 1.11 of bitt.tex 2021 Jul 27
*National Institutes of Health, National Cancer Institute, Center for Cancer Research, RNA Biology
Laboratory, P. O. Box B, Frederick, MD 21702-1201. (301) 846-5581; schneidt@mail.nih.gov;
https://alum.mit.edu/www/toms/
[1]
T. D.
Schneider.
Information
theory
primer,
with
an
appendix
on
logarithms.
Published
on
the
web,
2013,
2013.
https://doi.org/10.13140/2.1.2607.2000,
https://alum.mit.edu/www/toms/papers/primer/.
[2]
T. D.
Schneider.
Theory
of
molecular
machines.
I.
Channel
capacity
of
molecular
machines.
J.
Theor.
Biol.,
148:83–123,
1991.
https://doi.org/10.1016/S0022-5193(05)80466-7,
https://alum.mit.edu/www/toms/papers/ccmm/.
[3]
T. D.
Schneider.
Theory
of
molecular
machines.
II.
Energy
dissipation
from
molecular
machines.
J.
Theor.
Biol.,
148:125–137,
1991.
https://doi.org/10.1016/S0022-5193(05)80467-9,
https://alum.mit.edu/www/toms/papers/edmm/.
[4]
T. D.
Schneider
and
V. Jejjala.
Restriction
enzymes
use
a
24
dimensional
coding
space
to
recognize
6
base
long
DNA
sequences.
PLoS
One,
14:e0222419,
2019.
https://doi.org/10.1371/journal.pone.0222419,
https://alum.mit.edu/www/toms/papers/lattice/.
[5]
T. D.
Schneider.
70%
efficiency
of
bistate
molecular
machines
explained
by
information
theory,
high
dimensional
geometry
and
evolutionary
convergence.
Nucleic
Acids
Res.,
38:5995–6006,
2010.
https://doi.org/doi:10.1093/nar/gkq389,
https://alum.mit.edu/www/toms/papers/emmgeo/.
[6]
T. D.
Schneider.
A
brief
review
of
molecular
information
theory.
Nano
Communication
Networks,
1:173–180,
2010.
https://doi.org/10.1016/j.nancom.2010.09.002,
https://alum.mit.edu/www/toms/papers/brmit/.
[7]
T. D.
Schneider.
Sequence
logos,
machine/channel
capacity,
Maxwell’s
demon,
and
molecular
computers:
a
review
of
the
theory
of
molecular
machines.
Nanotechnology,
5:1–18,
1994.
https://doi.org/10.1088/0957-4484/5/1/001,
https://alum.mit.edu/www/toms/papers/nano2/.
[8]
J. B.
Johnson.
Thermal
agitation
of
electricity
in
conductors.
Physical
Review,
32:97–109,
1928.
https://doi.org/10.1103/PhysRev.32.97.
[9]
H. Nyquist.
Thermal
agitation
of
electric
charge
in
conductors.
Physical
Review,
32:110–113,
1928.
https://doi.org/10.1103/PhysRev.32.110.
[10]
T. D.
Schneider,
G. D.
Stormo,
L. Gold,
and
A. Ehrenfeucht.
Information
content
of
binding
sites
on
nucleotide
sequences.
J.
Mol.
Biol.,
188:415–431,
1986.
https://doi.org/10.1016/0022-2836(86)90165-8,
https://alum.mit.edu/www/toms/papers/schneider1986/.
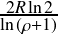 ≤ D <
≤ D < 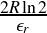
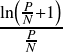 =
= 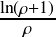
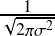 e-
e-