 A Horse Race to Beat Dembski's "Universal Probability Bound"
A Horse Race to Beat Dembski's "Universal Probability Bound"
As discussed in The AND-Multiplication Error, William Dembski claimed that there is a so-called "universal probability bound" which cannot be beaten, especially not by evolution:
"Randomly picking 250 proteins and having them all fall among those 500 therefore has probability (500/4,289)250, which has order of magnitude 10-234 and falls considerably below the universal probability bound of 10-150."
-- William Dembski, No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence. Rowman and Littlefield Publishers, Lanham Maryland, 2002. page 293
Let's see if we can obtain this "universal probability bound" using the Evj program. First we need to set things up:
Pu = 10-150so
-log2 Pu = 498.29 bitsCall it 500 bits.
| Parameter | Value |
|---|---|
| population: | 64 creatures |
| genome size: | 1024 bases |
| number of sites: | 60 |
| weight width: | 5 bases (standard) |
| site width: | 10 bases |
| mutations per generation: | 1 |
| Parameter | Value |
|---|---|
| population: | 64 creatures |
| genome size: | 2048 bases |
| number of sites: | 128 |
| weight width: | 5 bases (standard) |
| site width: | 10 bases |
| mutations per generation: | 4 |
| Parameter | Value |
|---|---|
| population: | 64 creatures |
| genome size: | 2048 bases |
| number of sites: | 128 |
| weight width: | 5 bases (standard) |
| site width: | 10 bases |
| mutations per generation: | 1 |
| Dembski's so-called "Universal Probability Bound" was beaten in an afternoon using natural selection! |
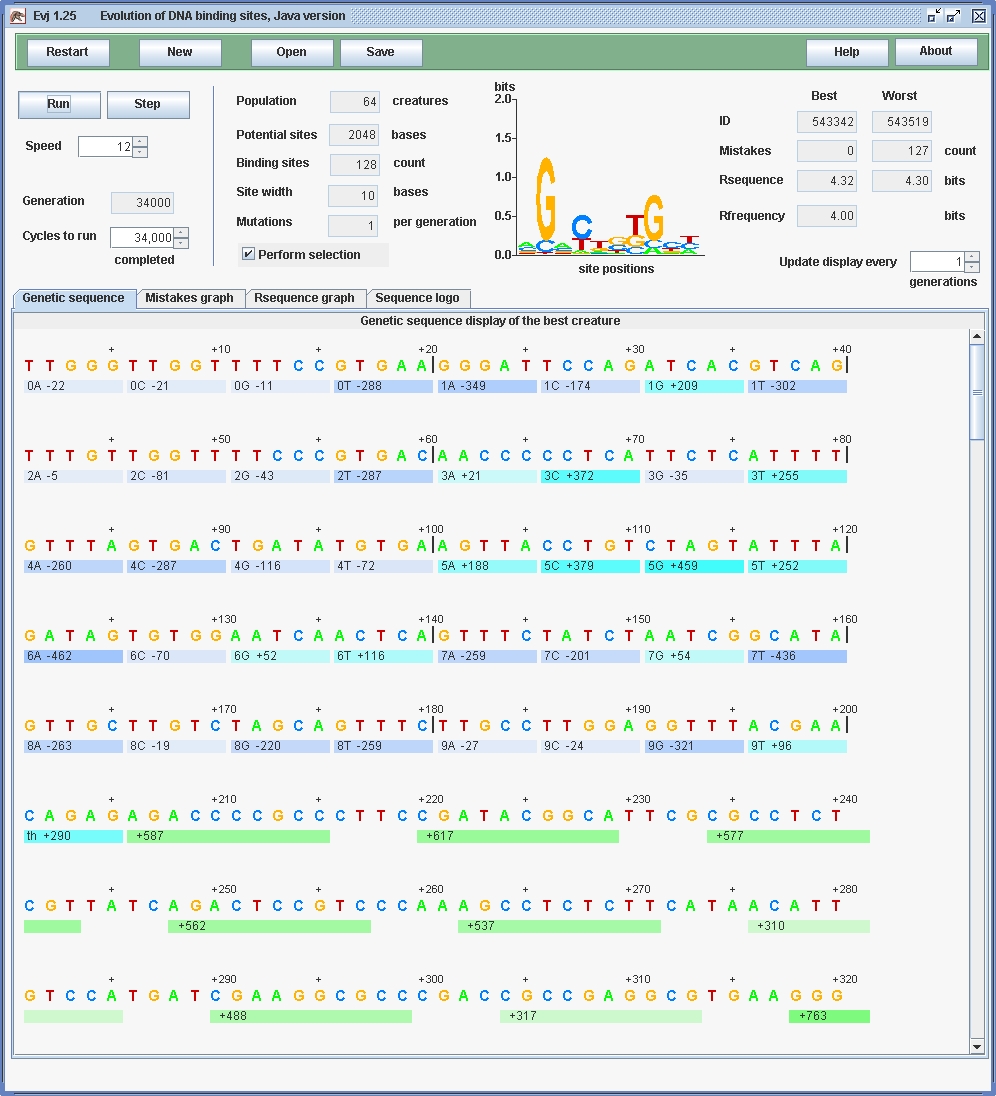
| Parameter | Value |
|---|---|
| population: | 512 creatures |
| genome size: | 2048 bases |
| number of sites: | 128 |
| weight width: | 5 bases (standard) |
| site width: | 10 bases |
| mutations per generation: | 1 |
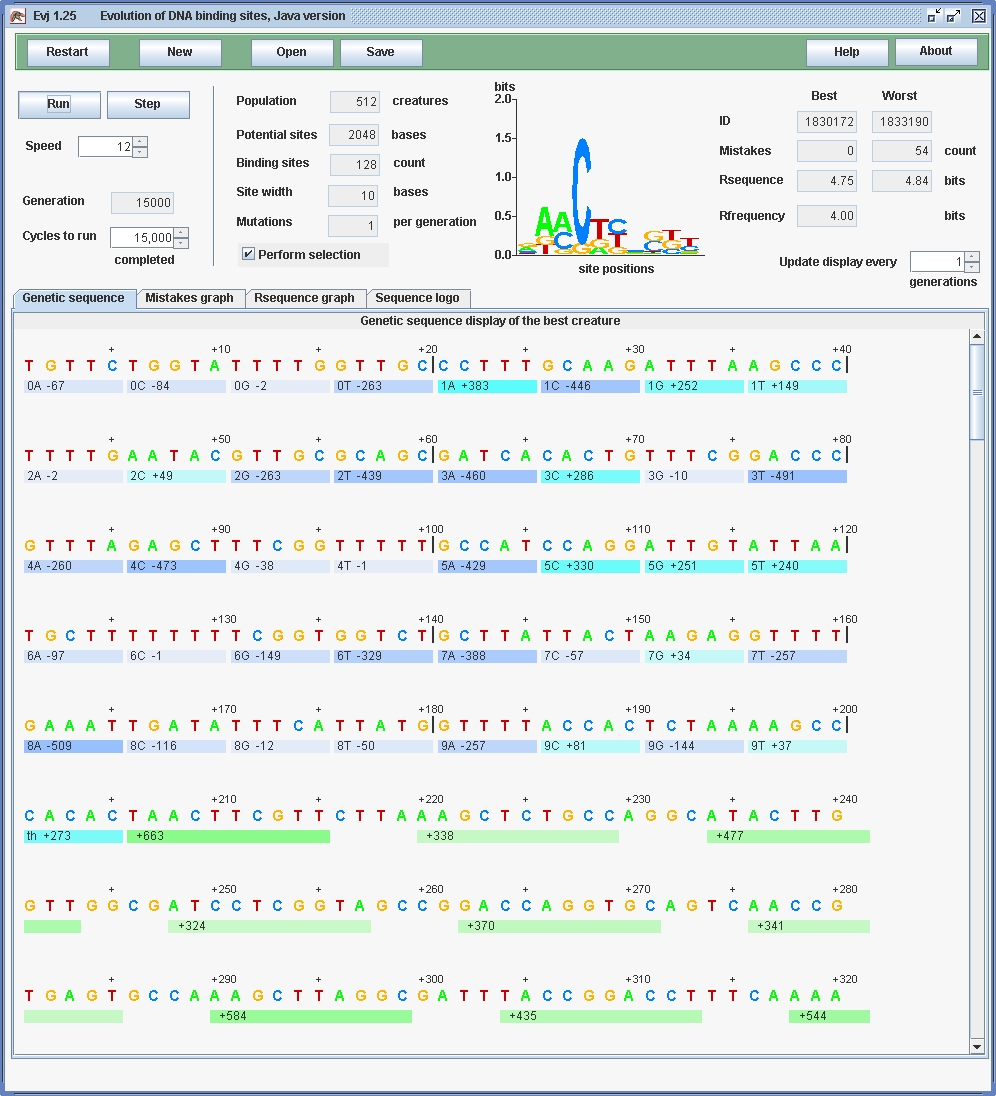
Can we really break way beyond Dembski's bound? By decreasing the site width, we can pack more sites in. The current Evj (version 1.25) has a limit of 200 sites:
| Parameter | Value |
|---|---|
| population: | 512 creatures |
| genome size: | 2048 bases |
| number of sites: | 200 |
| weight width: | 5 bases (standard) |
| site width: | 5 bases |
| mutations per generation: | 1 |
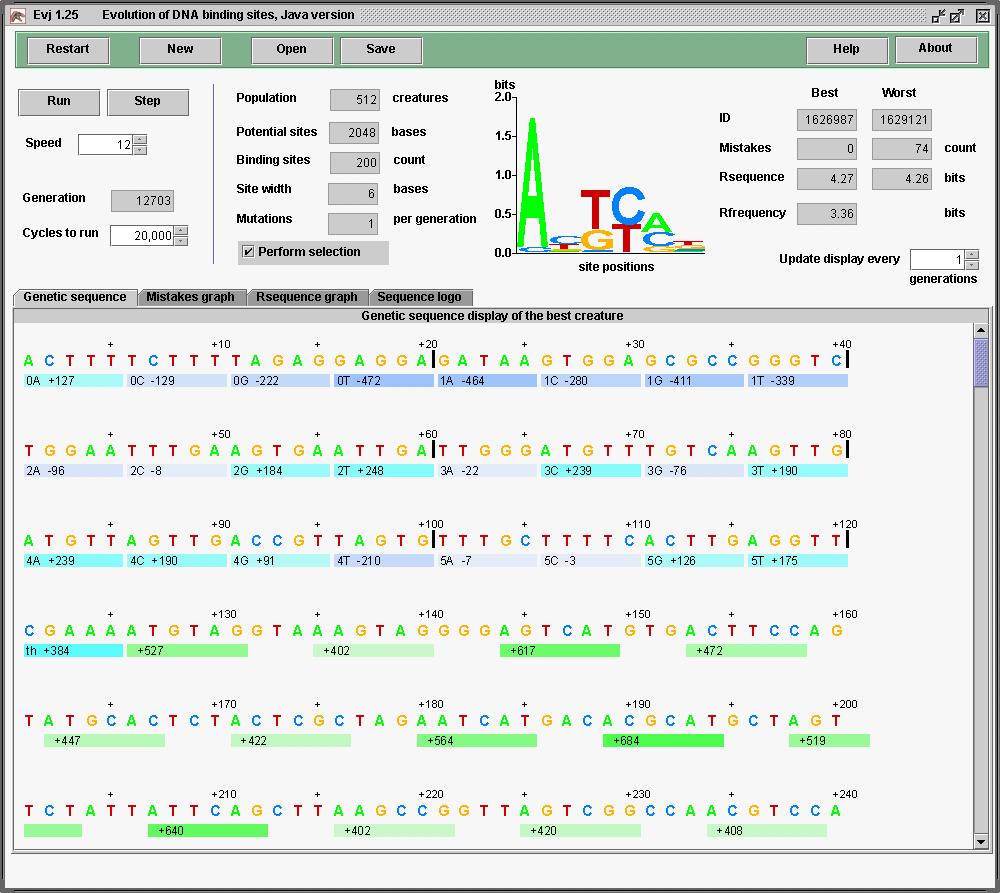 It looks a little different because I ran it on
a Mac G4, OSX 10.4.2, while the above were run on a Sun computer.
Java gives the same results on both.
It looks a little different because I ran it on
a Mac G4, OSX 10.4.2, while the above were run on a Sun computer.
Java gives the same results on both.
Let's go even further. Since Rfrequency = log2G/γ, can increase the information by increasing G. Evj 1.25 limits me to genomes of 4096. But that makes a lot of empty space where mutations won't help. So let's make the site width as big as possible to capture the mutations. ... no that takes too long to run. Make the site width back to 6 and max out the number of sites at 200. Rfrequency = 4.36 giving 871 bits.
| Parameter | Value |
|---|---|
| population: | 64 creatures |
| genome size: | 4096 bases |
| number of sites: | 200 |
| weight width: | 6 bases (standard) |
| site width: | 5 bases |
| mutations per generation: | 1 |
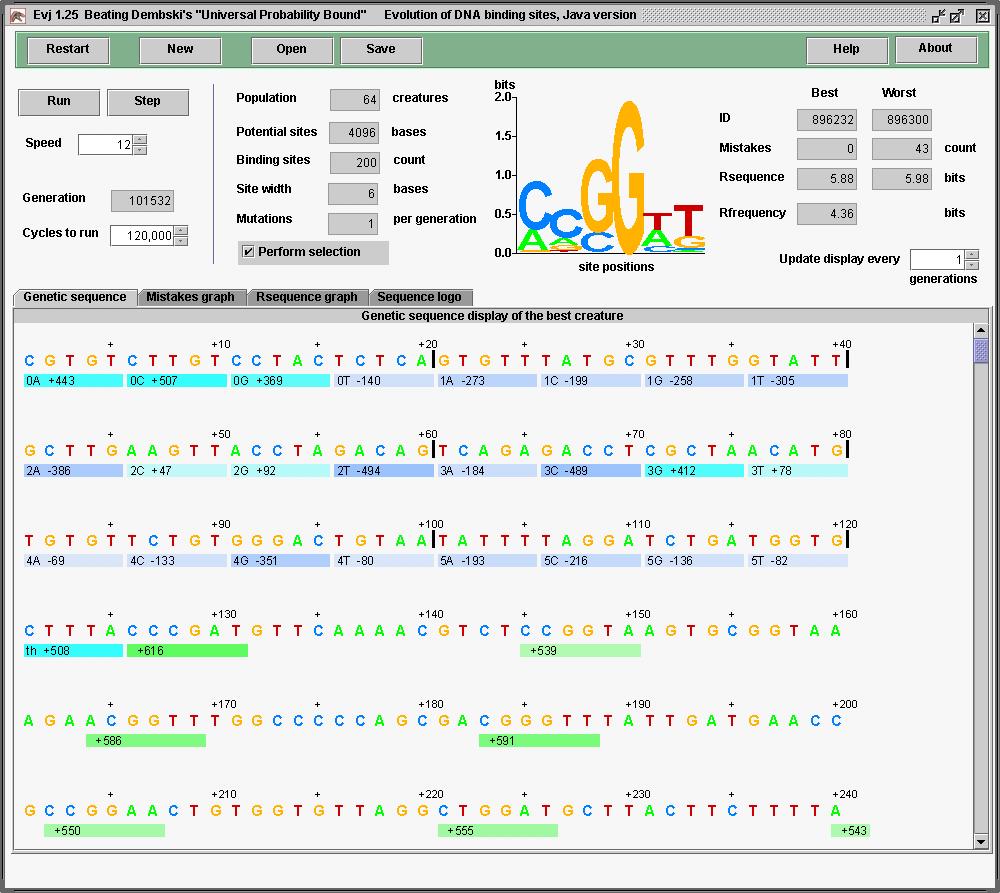 The probability of obtaining an 871 bit pattern
from random mutation (without selection of course) is
10-262, which beats Dembski's protein calculation
of
10-234 by
28 orders of magnitude.
This was done in perhaps an hour of computation with around 100,000 generations.
The probability of obtaining an 871 bit pattern
from random mutation (without selection of course) is
10-262, which beats Dembski's protein calculation
of
10-234 by
28 orders of magnitude.
This was done in perhaps an hour of computation with around 100,000 generations.
Dembski's claim that evolutionary processes cannot beat the "universal probability bound" are shown by Evj program runs to be false. It took a little while to pick parameters that give enough information to beat the bound, and some time was wasted with mutation rates so high that the system could not evolve. But after that it was a piece of cake.
Notice what I'm doing here. A lot of people say that Intelligent Design claims cannot be tested because they are not science. That's wrong, some of the claims can be tested. But as shown above, and elsewhere on this web site, the claims are demonstrably false. Therefore these claims will not become part of science.
I did learn an interesting lesson from this. (Note that I learned it, not the ID types!) The final binding sites take a long time to mutate because exact hits must be found in certain spots. Thus a high information content binding site may not appear rapidly. If we imagine that sites appear initially as a single control element, then they would have high information content. These would not evolve easily. So it seems more likely that gene duplication of the recognizer occurs, there is decay of the recognizer and that sites tend to have low information content initially. That means they would bind all over the genome and then the excess would be swept away gradually. Also, the threshold seems to restrict the finding of sites when it has a high value. So perhaps the evolution would run faster if one could force the threshold to zero. This is an option on our wish list and it probably simulates the natural situation closer.
![]()

Schneider Lab
origin: 2005 Oct 13
updated: 2012 Mar 08
![]()