Within 5 days of discovering that
![]() for a number of genetic systems
I found an apparent exception
[15].
The virus T7 infects
the bacterium
Escherichia coli and replaces the host RNA polymerase
with its own. These T7 polymerases bind to sites that have
about
Rsequence= 35.4 bits of information on the average.
If we compute
how much information is needed to locate the sites, it is only
Rfrequency= 16.5 bits.
So there is twice as much information at the sites as is needed
to find them.
for a number of genetic systems
I found an apparent exception
[15].
The virus T7 infects
the bacterium
Escherichia coli and replaces the host RNA polymerase
with its own. These T7 polymerases bind to sites that have
about
Rsequence= 35.4 bits of information on the average.
If we compute
how much information is needed to locate the sites, it is only
Rfrequency= 16.5 bits.
So there is twice as much information at the sites as is needed
to find them.
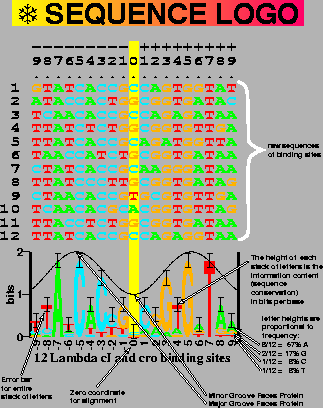
The idea that
![]() is the first hypothesis of molecular information theory.
As in physics if we are building a theory and we find a violation
we have two choices: junk the theory or recognize that we
have discovered a new phenomenon.
is the first hypothesis of molecular information theory.
As in physics if we are building a theory and we find a violation
we have two choices: junk the theory or recognize that we
have discovered a new phenomenon.
One possibility would be that the T7 polymerase really uses
all the information at its binding sites. I tested this idea
at the lab bench
by making many variations of the promoters and then seeing how
much information
is
left among those that still function
strongly. The result was ![]() bits [17],
which is reasonably close to
Rfrequency.
So the polymerase does not use all of the information available to
it in the DNA!
bits [17],
which is reasonably close to
Rfrequency.
So the polymerase does not use all of the information available to
it in the DNA!
An analogy, due to Matt Yarus, is that if we have a town
with 1000 houses we should expect to see
![]() digits
on each house so that the mail can be delivered.
(The analogy as is does not match the biology perfectly, but one
can change it to match
[3].)
Suppose we came across a town and we count 1000 houses but
each house has 6 digits on it. A simple explanation is that
there are two delivery systems that do not share
digits with each other.
digits
on each house so that the mail can be delivered.
(The analogy as is does not match the biology perfectly, but one
can change it to match
[3].)
Suppose we came across a town and we count 1000 houses but
each house has 6 digits on it. A simple explanation is that
there are two delivery systems that do not share
digits with each other.
In biological terms, this means that there could be another protein binding at T7 promoters. We are looking for it in the lab.
Some years after making this discovery, I asked one of my students, Nate Herman, to analyze the repeat sequences in a replicating ring of DNA called the F plasmid that makes bacteria male. (Yes, they grow little pilli ...) He did the analysis but did not do the binding sites I wanted because we were both ignorant of F biology at that time. Nate found that the incD repeats contain 60 bits of information but only 20 bits would be needed to find the sites. The implication is that three proteins bind there. Surprisingly, when we looked in the literature we found that an experiment had already been done that shows three proteins bind to that DNA [18,19]! It seems that we can predict the minimum number of proteins that bind to DNA.
 |