- ... Schneider1
Frederick Cancer Research and Development Center,
P. O. Box B,
Building 144, Room 469,
Frederick, MD 21702.
email address:
toms@alum.mit.edu
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
earlier!2
- The range
 was determined by using the Rsim program.
See [Stephens & Schneider, 1992].
was determined by using the Rsim program.
See [Stephens & Schneider, 1992].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pin.3
- Alternatively,
each vibrational mode of a molecule can
be thought of as corresponding to a pin. The important point
here is that there can be parts of a molecule consisting of groups
of atoms which move almost independently from the other groups.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... symmetric.4
-
The x and y axis projections of the polar coordinate point
are independent and normally distributed:
f(x) = e-x2
and
f(y) = e-y2. The combined distribution is
f(x, y) = e-x2 e-y2 =e-r2, where
x2 + y2 = r2. This is circularly distributed.
See [Schneider, 1991a] for further details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... energy?5
- At this
point, an anonymous reviewer asked why the problem was not phrased in terms of
``the resetting of the demon'' because this
is said to be the
important energy dissipating step
by people concerned with the limits of computation
[Leff & Rex, 1990].
To ``reset'' usually means to
set the state of a binary device to 0.
That requires choosing one
state from two since one could alternatively ``reset'' to 1.
Actually,
``resetting'' is a particular case of first adding
energy to a device
and then choosing a sub-state as the energy dissipates
into the surroundings.
This is what molecular machines do, but
the term ``reset'' generally does not fit well with
molecular machines operations.
For example, molecular biologists never say that
ribosomes ``reset'' themselves
when they bind to their sites. It is more sensible to speak
of them as making a choice or decision. Molecular biology forces
us to use this more general paradigm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
decrease.6
-
If
Hafter = 0, equation (17) collapses.
Unfortunately, this has fooled many authors into thinking
that equation (16) gives the information.
Because of equation (18), they then think that entropy
is proportional to information.
Thus a measure of ``disorder'' becomes associated with
``information'' and the confusion is complete. To avoid
this widespread error, always measure information as
a decrease in uncertainty.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... law.)7
-
Landauer's statement that ``throwing away information requires dissipation''
[Landauer, 1991] contradicts this form of the Second Law.
Suppose we have a binary device which can be either in a 0 or a 1 state.
Let us define
``erase'' and ``reset''
to mean to set the device to 0, starting from either the 0 or 1 state.
Since the device is stable in its initial state, whether 0 or 1,
we must add some energy to it to alter that state. This is called
``priming'' the machine [Schneider, 1991a].
From the excited state,
the device is guided by pre-set inputs
to fall into the 0 state, and hence it
must dissipate energy to the surroundings.
For example, to change the state of a coin requires that we
add some energy to rotate it.
Then
the coin can only come to rest again by giving up its rotational energy.
(Do not be fooled into thinking that a coin in the 0 state need not
go through this process because ``you'' can see it is in that state and save
yourself the trouble. Remember: you are not involved in the actual
operation of molecular machines, and even if you were, your seeing,
thinking and acting require energy dissipation! Specifically, to know that
the state is 0 requires a reading operation.)
Thus this second step of erasure looks
exactly the same as selecting a sub-state,
which is equivalent to an information gain of the device,
by the precise definition we use
[Schneider et al., 1986,Schneider, 1991b].
This is
not really so odd as it may seem, since we must do exactly the same
thing to set the device to 1. ``Erasing'' requires the same
process as filling
a memory with whatever information patterns we choose.
It is easy to demonstrate this--simply switch the labels
on each flip-flop
so that they all register zero.
Thus ``erasing''
consists of two steps: priming and setting.
Information in a memory is lost at the priming step,
and not at the energy dissipation step.
This is a direct restatement of the Second Law because
energy must be absorbed by the memory to destroy the information
there.
The energy is then dissipated to set the device and gain different
information.
Landauer's confusion came about
because he lumped the priming and the setting operations
into a single step, and because he did not take
care to rigorously define what he means by ``information''.
We can avoid the confusion by always describing these
steps explicitly, and by defining ``information''
as a difference in the
uncertainty state function [Schneider, 1991b].
Similar arguments apply even when the two states are at different
energy levels, as in a transistor [Mead & Conway, 1980].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
conditions.8
-
The fundamental importance of equation (26)
is not widely recognized.
Authors often loosely use the
phrase ``
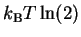 '' or even ``approximately
'' or even ``approximately
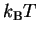 ''.
This leads to two difficulties.
First,
using disconnected mathematical phrases
has led people to overlook the idea that
they are part of an important equation.
Further, this equation has units: joules per bit.
If one chooses base 10 for measuring choices, one obtains
''.
This leads to two difficulties.
First,
using disconnected mathematical phrases
has led people to overlook the idea that
they are part of an important equation.
Further, this equation has units: joules per bit.
If one chooses base 10 for measuring choices, one obtains
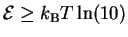 joules per digit.
For making calculations, it is necessary to keep the units in mind.
joules per digit.
For making calculations, it is necessary to keep the units in mind.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... configuration.9
- These
steps could be linked to save energy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... operation.10
- Feynman only counted output gates.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Easterns''.11
-
The originator of the method was E. M. Southern [Southern, 1975];
the later names are whimsical.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.