>



Next: (ii) Graphs of Rsequence
Up: (a) Calculation of Rsequence
Previous: (a) Calculation of Rsequence
Data for calculating
Rsequence comes from two sources. One is the
nucleotide sequences at which a recognizer has been shown to bind. The
other is the nucleotide composition of the genome in which
the recognizer functions. The sequences are aligned
by one base (the zero base) to give the largest
possible homology between them (see figure 9 for an example).
Some positions have little variation, while others have more. We
tabulate the frequency of each base B at each position L in the site,
to make
a table called f(B,L).
Focusing on one position at a time, we want to measure
the possible variations. For this we have chosen the "uncertainty" measure
introduced by Shannon in 1948 (Shannon, 1948; Shannon and Weaver, 1949;
Weaver, 1949;
Abramson, 1963; Singh, 1966; Gatlin, 1972; Sampson, 1976; Pierce, 1980;
Campbell, 1982; Schneider, 1984).
When there are M possible symbols, with
probabilities Pi (such that
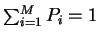 )
,
the general formula for uncertainty is
)
,
the general formula for uncertainty is
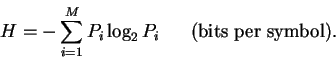 |
(1) |
One bit of information resolves the uncertainty of choice
between two equally likely symbols.
For nucleotide sequences, there are M=4 possible bases.
Using the frequencies of bases as estimates for probabilities,
the uncertainty is calculated as
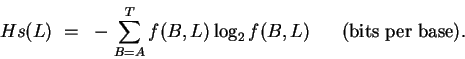 |
(2) |
(B is either A, C, G or T).
The formula gives sensible results
for three simple cases:
1) If only one base appears in the sequences, such
as an A, then f(A,L)=1 while the other frequencies are zero.
Hs(L) gives zero bits (
0 log 0 = 0),
meaning that if we were to sequence another site, we would have no
uncertainty that the next base will be an A.
2) If two bases appeared with equal frequency,
[as in
f(A,L)=0.5,
f(C,L)=0,
f(G,L)=0.5 and
f(T,L)=0], our uncertainty would be 1 bit.
3) If all 4 bases appeared with equal frequencies,
then
f(B,L)=0.25 and the uncertainty is 2 bits.
If we sequenced randomly in the genome,
and aligned sequences arbitrarily,
we would see all 4 bases, with probabilities P(B) and our
uncertainty about what base we would see next would be:
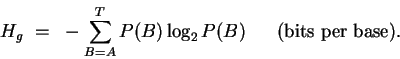 |
(3) |
This number is close to 2 bits for the organism E. coli,
considered in this paper.
In contrast, when sequences are aligned at binding sites
(as in typical consensus alignments)
a pattern appears which decreases the uncertainty
below that of randomly aligned fragments
(equation (2)).
For each position L the decrease would be:
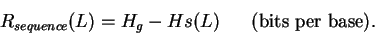 |
(4) |
This is a measure of the sequence information gained by aligning the sites.
The total information gained will be the total decrease in uncertainty:
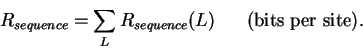 |
(5) |
(By summing, we make the simplifying assumption
that the frequencies at one position
are not influenced by those at another position. It is also possible to
calculate
Rsequencefrom dinucleotides or oligonucleotides [Shannon, 1951;
Gatlin, 1972; Lipman and Maizel, 1982].
When dinucleotides were used for ribosome
binding sites, the total information content was not
different from that given in Results, [unpublished observation].
Unfortunately, sampling error prevents one
from making the calculation in most cases.)



Next: (ii) Graphs of Rsequence
Up: (a) Calculation of Rsequence
Previous: (a) Calculation of Rsequence
Tom Schneider
2002-10-16
![]() )
,
the general formula for uncertainty is
)
,
the general formula for uncertainty is