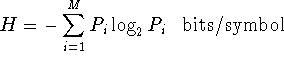On this page I report errors I found in:
@article {Tillman.Russel1961,
author = "F. Tillman
and B. R. Roswell",
title = "Information and entropy",
journal = "Synthese",
publisher = "Springer Netherlands",
issn = "0039-7857",
pages = "233--241",
volume = "13",
issue = "3",
url = "http://dx.doi.org/10.1007/BF00489885",
note = "10.1007/BF00489885",
comment = "Terrible paper, full of errors:
H = information, etc",
year = "1961"}
History.
A friend,
Ivan Erill
cited the above paper in
one of his nicely written documents about information theory.
Upon reading Tillman.Russel1961 I found many of the errors
listed on my page
Pitfalls in Information Theory
and
Molecular Information Theory.
Ivan asked that I post the list.
If a person falls into even one of the pitfalls, they
cannot get to
the rest of the theory.
Comments/corrections and discussion?
toms@alum.mit.edu
-
p. 233. "H amount of information". This is a common classical
error of not reading Shannon closely enough.
See Part II of
Shannon1948
where he discusses the formula for R:
... the rate of actual transmission, R, would be obtained by
subtracting from the rate of production (i.e., the entropy of the
source) the average rate of conditional entropy.
R = H(x) - Hy(x)
The conditional entropy Hy(x) will, for convenience, be
called the equivocation. It measures the average ambiguity of the
received signal.
For clarity, I call
H(x) the "uncertainty before" receiving the message (Hbefore)
and
Hy(x) the "uncertainty after" receiving the message (Hafter).
Information is measured as the decrease in uncertainty at the receiver
from before to after receiving the message.
Hafter is caused by noise in the system as Shannon discusses.
To confuse Hbefore with Hafter leads to a major pitfall.
-
p. 235. "That is, no physical measurement of the system could
determine which of the n states actually occurred." This is wrong -
technology moved forward and we can see the DNA sequences in binding
sites as states.
A great example can be seen by running the
Evj program.
Launch Evj
and set the speed to 21. Then click "Run".
The evolution completes in about 2-3 seconds.
The recognizer gene is marked by blue bars and
binding sites are marked by green bars.
Look at the bases between sites - they are fluctuating rapidly.
A single DNA sequence can be thought of as a snapshot of
the system.
-
p. 235. "The small differences which distinguish the n states one from
the other are supposedly too small to be detected."
50 years later we can see that this is wrong since
we now can observe single atoms and molecules in different states
using various techniques such as AFM and FRET.
-
p. 236. "An information source is not regarded as a physical system
according to Shannon's original definition."
No that's wrong.
Shannon was a practical engineer and had phone and radio systems
(which are obviously physical)
in mind all the time!
The more subtle point is that Shannon's measures are based on the
probabilities of states (or symbols or messages) of a system
and as
Pierce
pointed out, this is extremely general.
-
p. 236. "Brillouin defines information as (negative) entropy" also an
error since entropy is always positive.
That is, for the formula
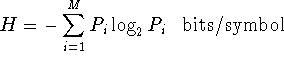 H >= 0.
H >= 0.
-
p. 236. spelling error: moecular
-
p. 237-238. "Brillouin has shown by detailed arguments that the
average decrease in entropy per symbol is given by the expression:
[-sum p log p]." That's wrong since the -sum p log p form is a state
function. One needs differences of them, as Shannon did!
-
p. 238. "In the definition of information, H, the p_i represent
probabilities of occurrence of distinguishable symbols whereas in the
definition of entropy, S, they represent probabilities of occurrence
of indistinguishable states of a physical system." This is silly when
one thinks about DNA sequences - they can't be opposites.
The authors are totally confused.
-
p. 238-239. "The information of standard English is not a physical
property of any system; it is most certainly not subject to the second
law of thermodynamics." Our data (in preparation) indicate that this is wrong.
-
p. 239. continuing from above, "If it were an entropy, then one could
predict with confidence that it would not decrease in the next
century. No one would make that mistake." No, that's like saying that
the entropy of binding sites must increase over time - but it doesn't
because there is selection for biological function. So they are just
wrong in this prediction.
-
p. 240. Use of 'negative entropy' shows complete confusion.
-
p. 240. "Physical laws do not apply to information, however." Wrong.
For example, C = W log2(P/N + 1) relates physical laws to information
since P is power and N is noise.
-
p. 240.
The entire page has one error after another.
I won't list them all.
Conclusion.
This paper is a great example of
pitfalls
in Molecular Information Theory.