Claude Elwood Shannon

Reprinted with permission of Alcatel-Lucent USA Inc.
April 30, 1916 --- February 24, 2001
Claude Elwood Shannon

April 30, 1916 --- February 24, 2001
Claude Elwood Shannon was born in Petoskey, Michigan, on April 30, 1916. He graduated with a B.S. in mathematics and electrical engineering from the University of Michigan in 1936. Shannon earned both a master's degree and a doctorate in 1940 as a student of Vannevar Bush at the Massachusetts Institute of Technology. At that time Vannevar Bush was vice president of M.I.T. and dean of the engineering school, and actively conducting research on his invention the differential analyzer, the first reliable analog computer that solved differential equations. Shannon's electrical engineering master's thesis "A Symbolic Analysis of Relay and Switching Circuits" has been described as one of the most important master's theses ever written. In it Shannon applied George Boole's binary (true-false) logic algebra found in Russell and Whitehead's Principia Mathematica to the problem of electronic (on-off) switching circuits. At the time, Boolean arithmetic was little known or used outside the field of mathematical logic. Because of Shannon's work, Boolean arithmetic is the basis for the design and operation of every computer in the world.
For his Ph.D. dissertation in mathematics, Shannon applied mathematics to genetics. This work was influenced by Norbert Wiener, one of his coworkers with Vannevar Bush at MIT. Wiener studied how the nervous system and machines perform the functions of communication and control, and as acknowledged by Shannon, Wiener made some early contributions to the field of information theory.
In 1941, Shannon joined Bell Telephone Laboratories in New Jersey as a research mathematician. While working on the problem of efficiently transmitting communications, he formulated a theory quantifying information. "The Mathematical Theory of Communication" (Bell System Technical Journal, 1948) extended the concept of entropy (a measure of uncertainty) by demonstrating that decreases in uncertainty correspond to the information content in a message. This paper began the field of Information Theory. In footnotes of the 1949 book reprinting the 1948 paper, Shannon and Warren Weaver acknowledge that their work was based on the treatment of "information" by John von Neumann in 1932, Leo Szilard in 1929, R.V.L. Hartley in 1928, and ultimately to Gibbs 1902 work in statistical mechanics and Boltzmann's 1894 work in thermodynamics. The most important concept of Shannon's theory is the "entropy function". It is expressed in the discrete form by the equation
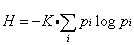
This function represents the lower limit on the expected number of symbols required to code for the outcome of an event regardless of the method of coding, and is thus the unique measure of the quantity of information. It is the amount of information that would be required to reduce the uncertainty about an event with a set of probable outcomes to a certainty. As derived by Shannon it is the only measure of information that simultaneously meets the three conditions of being continuous over the probability, of monotonically increasing with the number of equiprobable outcomes, and of being the weighted sum of the same function defined on different partitions of the probable outcomes. In the discrete and continuous forms, the uncertainty corresponds to the entropy of statistical mechanics and to the entropy of the second law of thermodynamics, and it is the foundation of information theory. Shannon's work has found application in computer science, in communication engineering, in biological information systems including nucleic acid and protein coding, and hormonal and metabolic signaling, in linguistics, phonetics, cognitive psychology, and cryptography.
In his work Shannon used this measure of information to show how many extra bits would be needed to efficiently correct for errors when the message was transmitted on a noisy channel. This work was critical for the development of digital encoding and modern electronic communications. Shannon's papers also contain the first use of the word "bit" as shorthand for "the binary digit."
At Bell Labs Shannon was known for his eclectic interests, and for his dexterity both at constructing devices and at juggling and riding his unicycle down the halls. He remained affiliated with the Labs until 1972. He returned to MIT as a visiting professor in 1956, as a permanent member of the faculty in 1958, and as a professor emeritus in 1978. His work on chess-playing machines and an electronic mouse that could "learn" to run a maze helped create the field of artificial intelligence.
Dr. Shannon died on Saturday, February 24, 2001, in Medford, Mass. He had been afflicted with Alzheimer's disease for several years. Dr. Marvin Minsky of M.I.T. said that despite the effects of the illness "the image of that great stream of ideas still persists in everyone his mind ever touched."
For a bibliography, see the Bio-Info FAQ Shannon Bibliography.
Written by John S. Garavelli, Thomas D. Schneider, and John L. Spouge.
![]()
Shannon Statue
![]()

Schneider Lab
origin: 2001 Feb 28
updated: 2018 Jul 06
![]()