To test the hypothesis that Rsequence can evolve to match Rfrequency, the evolutionary process was simulated by a simple computer program, ev, for which I will describe one evolutionary run. This paper demonstrates that a set of 16 binding sites in a genome size of 256 bases, which would theoretically be expected to have an average of Rfrequency = 4 bits of information per site, can evolve to this value given only these minimal numerical and size constraints. Although many parameter variations are possible, they give similar results as long as extremes are avoided (data not shown).
A small population (n=64) of `organisms'
was created, each of which consisted of G= 256 bases of nucleotide
sequence chosen randomly, with equal probabilities,
from an alphabet of 4 characters
(a, c, g, t,
Fig. 1).
At any particular time in the history of a natural population,
the size of a genome, G, and the number of
required genetic control element binding sites, ![]() ,
are determined
by previous history and current physiology respectively, so
as a parameter for this simulation
we chose
,
are determined
by previous history and current physiology respectively, so
as a parameter for this simulation
we chose
![]() and
the program arbitrarily chose the site locations, which are
fixed for the duration of the run.
The information required to locate
and
the program arbitrarily chose the site locations, which are
fixed for the duration of the run.
The information required to locate ![]() sites in a genome
of size G is
sites in a genome
of size G is
![]() bits
per site, where
bits
per site, where ![]() is the frequency of
sites [4,14].
is the frequency of
sites [4,14].
A section of the genome is set aside by the program to encode the gene for a sequence recognizing `protein', represented by a weight matrix [15,7] consisting of a two-dimensional array of 4 by L = 6 integers. These integers are stored in the genome in twos complement notation, which allows for both negative and positive values. (In this notation, the negative of an integer is formed by taking the complement of all bits and adding 1.) By encoding A=00, C=01, G=10, and T=11 in a space of 5 bases, integers from -512 to +511 are stored in the genome. Generation of the weight matrix integers from the nucleotide sequence gene corresponds to translation and protein folding in natural systems. The weight matrix can evaluate any L base long sequence. Each base of the sequence selects the corresponding weight from the matrix and these weights are summed. If the sum is larger than a tolerance, also encoded in the genome, the sequence is `recognized' and this corresponds to a protein binding to DNA (Fig. 1). As mentioned above, the exact form of the recognition mechanism is immaterial because of the generality of information theory.
The weight matrix gene for an organism is translated
and then every position of that organism's genome is evaluated by the matrix.
The organism can make two kinds of `mistakes'.
The first is for one of the ![]() binding locations to be
missed (representing absence of genetic control)
and the second is for one of the
binding locations to be
missed (representing absence of genetic control)
and the second is for one of the
![]() non-binding sites to be incorrectly recognized
(representing wasteful binding of the recognizer).
For simplicity these mistakes are counted as equivalent,
since other schemes should give similar final results.
The validity of this black/white model of binding sites comes
from Shannon's channel capacity theorem, which allows for recognition with as
few errors as necessary for survival [1,16,7].
non-binding sites to be incorrectly recognized
(representing wasteful binding of the recognizer).
For simplicity these mistakes are counted as equivalent,
since other schemes should give similar final results.
The validity of this black/white model of binding sites comes
from Shannon's channel capacity theorem, which allows for recognition with as
few errors as necessary for survival [1,16,7].
The organisms are subjected to rounds of selection and mutation. First, the number of mistakes made by each organism in the population is determined. Then the half of the population making the least mistakes is allowed to replicate by having their genomes replace (`kill') the ones making more mistakes. (To preserve diversity, no replacement takes place if they are equal.) At every generation, each organism is subjected to one random point mutation in which the original base is obtained 1/4 of the time. For comparison, HIV-1 reverse transcriptase makes about one error every 2000-5000 bases incorporated, only 10 fold lower than this simulation [17].
When the program starts, the genomes all contain random sequence,
and the information content of the binding sites,
Rsequence, is close to zero.
Remarkably, the cyclic mutation and selection process leads to
an organism that makes no mistakes in only 704 generations
(Fig. 2a).
Although the sites can contain a maximum of 2L = 12 bits,
the information content of the binding sites rises during this
time until it oscillates around the predicted information content,
Rfrequency = 4 bits, with
![]() bits
during the 1000 to 2000 generation interval
(Fig. 2b).
The expected standard deviation from small sample
effects [4] is 0.297 bits,
so about 55% of the variance (
0.32/0.42) comes from the digital
nature of the sequences.
Sequence logos [5]
of the binding sites show that distinct
patterns appear during selection, and that
these then drift
(Fig. 3).
When selective pressure is removed, the observed
pattern atrophies (not shown, but Fig. 1 shows the
organism with the fewest mistakes
at generation 2000,
after atrophy)
and the information content drops back to zero
(Fig. 2b).
The information decays with a half-life of 61 generations.
bits
during the 1000 to 2000 generation interval
(Fig. 2b).
The expected standard deviation from small sample
effects [4] is 0.297 bits,
so about 55% of the variance (
0.32/0.42) comes from the digital
nature of the sequences.
Sequence logos [5]
of the binding sites show that distinct
patterns appear during selection, and that
these then drift
(Fig. 3).
When selective pressure is removed, the observed
pattern atrophies (not shown, but Fig. 1 shows the
organism with the fewest mistakes
at generation 2000,
after atrophy)
and the information content drops back to zero
(Fig. 2b).
The information decays with a half-life of 61 generations.
The evolutionary steps can be understood by considering an intermediate situation, for example when all organisms are making 8 mistakes. Random mutations in a genome that lead to more mistakes will immediately cause the selective elimination of that organism. On the other hand, if one organism randomly `discovers' how to make 7 mistakes, it is guaranteed (in this simplistic model) to reproduce every generation, and therefore it exponentially overtakes the population. This roughly-sigmoidal rapid transition corresponds to (and the program was inspired by) the proposal that evolution proceeds by punctuated equilibrium [18,19], with noisy `active stasis' clearly visible from generation 705 to 2000 (Fig. 2b, Fig. 3).
An advantage of the ev model over previous evolutionary models, such as biomorphs [20], Avida [21], and Tierra [22], is that it starts with a completely random genome, and no further intervention is required. Given that gene duplication is common and that transcription and translation are part of the housekeeping functions of all cells, the program simulates the process of evolution of new binding sites from scratch. The exact mechanisms of translation and locating binding sites are irrelevant.
The information increases can be understood
by looking at the equations used to compute the information
[12].
The information in the binding sites is measured as
the decrease in uncertainty from before binding to after
binding [4,14]:
Before binding the uncertainty is
| Hbefore = Hg L | (2) |
where L is the site width,
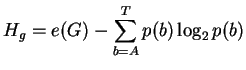 ,
e(G) is a small sample correction [4]
and p(b) is the frequency of base b in the genome of size G.
After binding the uncertainty is:
,
e(G) is a small sample correction [4]
and p(b) is the frequency of base b in the genome of size G.
After binding the uncertainty is:
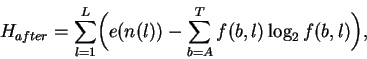 |
(3) |
where f(b,l) is the frequency of base b at position l in the binding sites and e(n(l)) is a small sample size correction [4] for the n(l) sequences at l. In both this model and in natural binding sites, random mutations tend to increase both Hbeforeand Haftersince equiprobable distributions maximize the uncertainty and entropy [1]. Because there are only 4 symbols (or states), nucleotides can form a closed system and this tendency to increase appears to be a form of the Second Law of Thermodynamics [23,12], where H is proportional to the entropy for molecular systems [24]. Effective closure occurs because selections have little effect on the overall frequencies of bases in the genome, so without external influence Hbefore maximizes at
Microevolution can be measured in haldanes, as standard deviations
per generation
[25,26,27].
In this simulation
![]() bits evolved at each site
in 704 generations, or
bits evolved at each site
in 704 generations, or
![]() haldanes.
This is within the range of natural population change,
indicating that although selection is strong, the model
is reasonable.
However,
a difficulty with using standard deviations is that they
are not additive for independent measures, whereas bits are.
A measure suggested by Haldane is the darwin,
the natural logarithm of change per million years, which has
units of nits per time.
This is the rate of
information transmission originally introduced by Shannon
[1].
Because a computer simulation does not correlate with time,
the haldane and darwin can be combined
to give units of bits per generation,
in this case
haldanes.
This is within the range of natural population change,
indicating that although selection is strong, the model
is reasonable.
However,
a difficulty with using standard deviations is that they
are not additive for independent measures, whereas bits are.
A measure suggested by Haldane is the darwin,
the natural logarithm of change per million years, which has
units of nits per time.
This is the rate of
information transmission originally introduced by Shannon
[1].
Because a computer simulation does not correlate with time,
the haldane and darwin can be combined
to give units of bits per generation,
in this case
![]() bits per generation per site.
bits per generation per site.