Sphere packing in 2 and higher dimensions

Geometry for optimal bistate molecular machines.

lattice: Restriction enzymes use a 24 dimensional coding space to recognize 6 base long DNA sequences
  Thomas D. Schneider and Vishnu Jejjala

Cell phones and molecules face the same task: figuring out a signal in the presence of overwhelming noise.

This is the story of why your cell phone gives you such a clear signal that you don't realize that it is fighting to figure out the desired signal from noisy electrical interference. It is also the story of how a tiny protein molecule can find exactly one sequence on DNA, such as GAATTC, despite noisy interference in that task by being bombarded by the surrounding water molecules and ions. Mathematically they are the same story.

When you talk on your cell phone, a signal comes from the other person into the electronics. The signal initially is clean voltage pulses, e.g. exactly 1 and 0 volts. But by the time it gets to your phone it is degraded by noise. Heat in the wires, called thermal noise, kicks electrons to higher or lower energy. A series of kicks happen before you get each pulse. So sometimes you would get 1.1 volts, another time 0.98 and so on. There is a law in statistics called the "central limit theorem" that says that whenever a large number of random values are added together, the distribution will follow a "bell shaped curve" (also known more precisely as a Normal or Gaussian distribution). So if you made a histogram of the voltages of the pulses, you would get a Gaussian distribution.

If you were to receive a long message and measure the voltage for every 0 pulse sent, a graph of the pulse voltages you observe would be Gaussian along a line, centered at zero volts. Likewise, the 1 pulses would also be Gaussian, but centered at 1 volt.

Now consider the first two pulses of a message. Each pulse and its noise is independent from the other pulse. Geometrically two independent values can be plotted at right angles. It turns out that the distribution of two Gaussian distributions combined is circularly symmetric. (You can work out why that is as homework or you can read at https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1538977/ or https://alum.mit.edu/www/toms/papers/shannonbiologist/ - see the box, "Representing a message as a hypersphere.") That is, it's a fuzzy circle. With three pulses, one gets a spherical distribution. With four pulses ... it's a 4 dimensional "hypersphere". Don't panic! Just think in three dimensions and do mathematics to figure out details. It turns out that as one keeps adding pulses, the distribution becomes more and more like a ping pong ball with everything on the surface (See https://alum.mit.edu/www/toms/papers/ccmm/ for the mathematical details.)

So how best to pack spheres together? In two dimensions one could put coins down in a square array, but we all know that they pack together better if one uses a hexagonal array 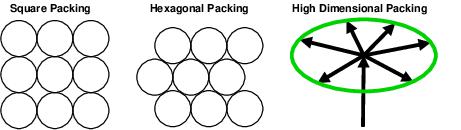(See the first figure in our paper at https://doi.org/10.1371/journal.pone.0222419). A pile of oranges in a food store is the best way to pack spheres in three dimensions.

For our paper, we are interested in understanding how biological molecules work. It turns out that they use exactly the same mathematics as Shannon developed for communications, information and coding theory.

The protein EcoRI binds to DNA at the sequence GAATTC. To describe this using information theory, just think about the first base, 'G'. That is one of four possibilities. Now simplify the problem to just head's and tails of a coin. If I have a coin on a table with heads or tails facing up but you don't see it, you would have to ask me one question "is it heads" and I would answer yes or no. That tells you one bit of information. In the case of DNA there are four possibilities, A, C, G and T so you could ask two questions: "Is it in the set G or A?" and "Is it in the set G or T?" My two answers tell you 2 bits of information.

We can do this for all 6 positions in the binding site GAATTC. Then the total number of bits is 6 (positions per site) x 2 (bits per position) = 12 (bits per site) since bits can be added, a property of information that Shannon initially required of the mathematics.

An invading virus will inject its DNA into a bacterium and take over the cell. Bacteria have developed a defense that "restricts" the growth of the virus. These are the restriction enzymes. After the virus has injected its DNA into a bacterium, EcoRI molecules inside the cell will bind to the DNA and cut it at GAATTC. This destroys the virus and so protects the bacterium.

EcoRI essentially does not cut at any other sequence, and so it is a useful reagent for genetic engineering that we use for cutting up DNA. For EcoRI to bind to GAATTC, it needs a set of specific contacts to the DNA. It's like a key in a lock. The lock has a number of two-part pins that move up and down based on the key. If it's the right key, the pins move so that the break between the pins are all at the shear line and the lock can open. If two pins were to move together, then the lock would be less secure because it would be easier to pick. So the pins should move independently. But that means that the state of the lock can be described by a set of independent numbers and therefore a lock is a high dimensional device.

So how many 'pins' does EcoRI have? That is, how many dimensions does EcoRI work in? That's what our paper answers. I got the an equation for the dimensionality in 1994. When I showed the equation to Vishnu Jejjala, who was a high school student working with me at that time, he said several smart things. First, he noted that the equation is a lower bound on the dimensionality. Unfortunately, having a lower bound is disappointing because the higher the dimension, the sharper the spheres are (more like a ping pong ball instead of a fuzzy ball of yarn). So in biology we would expect a very high dimensionality and a lower bound is useless. But then Vishnu suggested that there might also be an upper bound equation and that the two equations might converge to give a single answer to the what the dimensionality is.

18 years later (!) I was reading a paper by Jaynes. He knew that muscle is 70% efficient but the only tool he had to think about that was the Carnot efficiency. This is the efficiency of a heat engine as in a car. It uses a high temperature (burning fuel) and a low temperature (the outside air) to drive the engine. Carnot's equation does not apply to biological systems because those work at one temperature.

For example, by holding onto the negative charge of the DNA backbone, EcoRI can glide along DNA like a train on spiral tracks. Before EcoRI is bound to DNA, it is somewhere along the DNA. It quickly goes to equilibrium with the surrounding water. That is, it is at the same temperature as the water. Because it gets kicked around by thermal noise, EcoRI moves along the DNA by random Brownian motion and eventually when it encounters a GAATTC sequence, it forms contacts and binds there. For it to stick, energy must be dissipated out into the surrounding water. The amount of energy can be measured using a microcalorimeter. To get some idea about how fast the energy leaves the EcoRI/DNA complex, I looked into the speed of sound in sea water. It turns out that it takes about a picosecond for sound to cross the diameter of DNA. So in a few picoseconds the heat will go away and the EcoRI will be bound to the DNA at the temperature of the surroundings. The temperature before binding (Th) is the same as the temperature after binding (Tc). As a result the Carnot efficiency ((Th - Tc)/Th) is zero, so that's not the right way to measure the efficiency.

It turns out that there is an equation developed from Shannon's work (the channel capacity equation) by Pierce and Cutler and published in 1959 that can be used when the temperature is constant - an isothermal efficiency. Pierce wrote the best introduction to information theory (Symbols Signals And Noise https://archive.org/details/symbolssignalsan002575mbp). Cutler was my father's boss at Bell Labs. (I met him once when I was perhaps 5 - he was as tall as a two story building and had white hair.) I used that efficiency equation and hypersphere packing to explain why many molecules, including EcoRI and the light sensitive protein in your eye rhodopsin, are 70% efficient (see https://alum.mit.edu/www/toms/papers/emmgeo/).

So when I saw the paper in which Jaynes was trying to use the Carnot equation for muscle, I knew he was doomed. But I eagerly read the paper to see how he would handle it and he did indeed fail because he didn't have the Pierce / Cutler equation for isothermal efficiency. But Jaynes was not stupid. He wrote so clearly that he lucidly explained an equation for noise that I had already for 20 years. His explanation led me to realize that the noise equation could be rearranged to determine an upper bound for the dimensionality. Vishnu was right, there really is an equation for an upper bound!

A few manipulations made both the lower and upper bounds look really similar - a rather mysterious result - and when one asks how they would evolve to get to 70% efficiency ... the upper and lower bounds converge to a spectacularly simple answer: twice the information measured in bits. So the 12 bit GAATTC that EcoRI binds to means it works in 24 dimensions.

Again, Vishnu was right - the bounds converge. Essentially he was my mentor all those years.

Since Shannon developed his theory of packing of high dimensional spheres in 1949 people have been busy figuring out the best ways to pack spheres in various dimensions. It turns out that the very best way to pack spheres is called the Leech lattice, and it is in 24 dimensions.

In other words, we believe that EcoRI probably uses a Leech lattice to find its binding sites precisely. This implies that we might be able to build the noise decoder in cellphones using a single molecule.