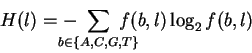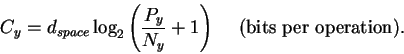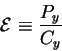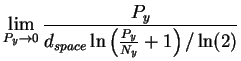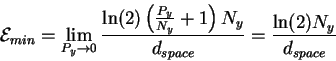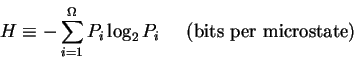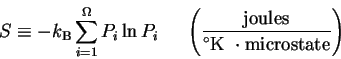Abstract
Living cells contain many molecules which can make simple decisions, such as whether to bind to a particular nucleotide sequence or not. A theory describing the practical limits of these molecular machines is reviewed. Level 0 theory uses Shannon's information theory to study genetic control systems. Level 1 theory uses Shannon's channel capacity theorem to explain how these biological molecules are able to make their decisions precisely in the face of the thermal maelstrom surrounding them. Level 2 theory shows how the Second Law of Thermodynamics defines the exact extent of the choices available to a molecular machine when it dissipates a given amount of energy. Even the famous Maxwell demon must obey this result. The theory also has implications for designing molecular computers.
1. Introduction
The idea of nanotechnology is founded on the premise that it will be possible to construct machines with atomic scale precision [Feynman, 1961,Drexler, 1981,Drexler, 1986]. Biology provides many examples that this is possible; we ``merely'' need to learn what has been achieved by evolution and to copy it. But eventually we must determine what the engineering limitations of molecular machines are. What should we attempt and what would be foolish to try to violate? This paper reviews a general theory of molecular machines which begins to address this question. The theory is divided into several hierarchal levels.
First, to get a good grasp on these problems, we need practical examples which we can play with in the lab. Because genetic control systems read linear sequences of nucleotides, they provide us with easy access to their coded structure. Level 0 molecular machine theory shows how we can use these systems to study information processes at the molecular level. We will show how we have used information theory [Pierce, 1980,Shannon, 1948,Shannon & Weaver, 1949,Sloane & Wyner, 1993] to dissect the operation of molecular machines [Schneider et al., 1986,Schneider, 1988,Schneider & Stormo, 1989,Schneider & Stephens, 1990,,Stephens & Schneider, 1992,Papp et al., 1993]. Other groups are now using these techniques to study a variety of molecular systems [Berg & von Hippel, 1987,Mars & Beaud, 1987,Berg & von Hippel, 1988,Eiglmeier et al., 1989,Stormo, 1990,Fields, 1990,,Penotti, 1991,Shenkin et al., 1991,Day, 1992].
Level 1 theory [Schneider, 1991a] explains the amazingly precise actions taken by these molecules. For example, the restriction enzyme EcoRI scans across double helical DNA (the genetic material) and cuts almost exclusively at the pattern 5' GAATTC 3', while avoiding the 46 - 1 = 4095 other 6 base pair long sequences [Polisky et al., 1975,Woodhead et al., 1981,Pingoud, 1985]. How EcoRI is able to do this has been somewhat of a mystery because conventional chemical explanations have failed [Rosenberg et al., 1987]. According to level 1 theory, molecular machines such as EcoRI are constrained in their operations by their ``machine capacity'', which is closely related to Claude Shannon's famous ``channel capacity'' [Shannon, 1949]. So long as one does not exceed the channel capacity, Shannon's theorem guarantees that one may have as few errors in communication as desired. It is this theorem which has led to spectacularly clear telephone communications and compact disk (CD) sound recordings. The equivalent statement for molecular machines is that, so long as a molecular machine does not exceed its machine capacity, it may take actions as precise as may be required for evolutionary survival. We will sketch the proof of this amazing result.
Level 2 theory [Schneider, 1991b] deals with the ancient problem of
Maxwell's demon [Leff & Rex, 1990] and shows that there is an energetic cost to
molecular operations: at least
![]() joules must be dissipated
to the surroundings for every bit of information gained
by the machine
(where
joules must be dissipated
to the surroundings for every bit of information gained
by the machine
(where
![]() is Boltzmann's constant and T is the temperature in kelvin).
In the recent literature
some authors often
claim that
is Boltzmann's constant and T is the temperature in kelvin).
In the recent literature
some authors often
claim that
![]() is not a limit at all or that
information loss (rather than gain) is associated with dissipation
[Landauer, 1991].
However, this relationship is merely (!) a restatement of
the Second Law of Thermodynamics [Schneider, 1991b], so those who contest it
are unlikely to be correct.
We will investigate the source of this confusion.
is not a limit at all or that
information loss (rather than gain) is associated with dissipation
[Landauer, 1991].
However, this relationship is merely (!) a restatement of
the Second Law of Thermodynamics [Schneider, 1991b], so those who contest it
are unlikely to be correct.
We will investigate the source of this confusion.
Finally, we discuss the implications of these results for the prospects of constructing our own molecular machines and molecular computers [Bradley, 1993].
The purpose of this review is to provide a meeting ground for biologists, physicists, computer scientists and electrical engineers. Unfortunately ideas that are famous in one field are unknown in another. Sadly, modern science is now so fragmented that few people know both what a bit is and what translation is. Rather than turn this review into a book, I encourage the reader to read Pierce (1980) for background on information theory, and Watson (1987) or Gonick (1983b) for excellent introductions to molecular biology. Only the central ideas and results of the theory of molecular machines are reviewed in this paper, so only some mathematical equations are presented. Detailed derivations may be found in the references.
2. Level 0 Molecular Machine Theory: Nucleic Acid Binding Molecules as
Practical Examples
A ribosome is a collection of proteins and RNAs which reads messenger RNA and uses that information to construct proteins. This translation process starts in a region called the ribosome binding site [Gold et al., 1981,Stormo et al., 1982b]. One problem facing ribosomes is to locate the binding sites. The cell's survival depends on how well this is done. Some genes are crucial because the translated protein is required for an important cellular function. Other proteins are needed for efficiency, and so the loss of them would put the organism at a competitive disadvantage. If a protein were unnecessary, mutations in its gene would eventually destroy it, and the ribosome binding site at the start of the gene would atrophy. Likewise, if the ribosome were to start translation in places that it shouldn't, the cell would waste energy making useless proteins. Thus it would make biological sense if the only places ribosome binding sites exist is in front of functional genes. However, the conventional wisdom of biologists and chemists says that this is not possible because chemical reactions can have many side products, and only a portion of the substrate becomes product. Thus in the chemists way of thinking, the ribosome can begin translation just about anywhere, with a smooth gradation between real sites and other places. In contrast, information theory says that precise choices (distinguishing sites from non-sites) can be made by the appropriate combination of many ``sloppy'' components. Whether such precise recognition is actually done is a question which can only be answered experimentally.
The bacterium Escherichia coli has approximately 2600 genes
[Schneider et al., 1986],
each of which starts with a ribosome binding site.
These have to be located from about 4.7 million bases of RNA
which the cell can produce [Kohara et al., 1987].
So the problem is to locate 2600 things from a set of
![]() possibilities, and not make any mistakes.
How many choices must be made?
possibilities, and not make any mistakes.
How many choices must be made?
The solution to this question,
![]() bits, is ``obvious'' to those of
us versed in information theory, but the reasoning behind how
this works in a biological system
is subtle and not obvious, so
let's consider a simpler example
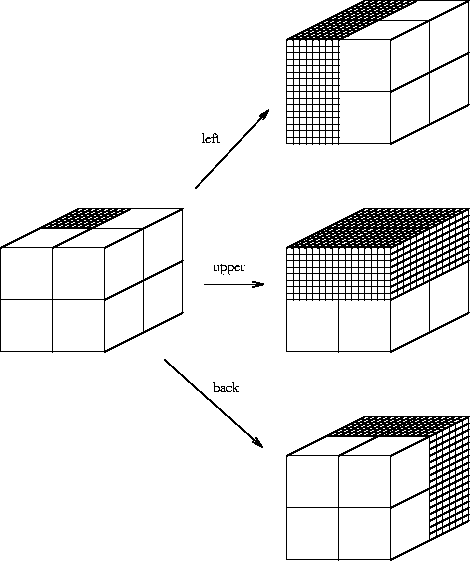
(Fig. 1).
bits, is ``obvious'' to those of
us versed in information theory, but the reasoning behind how
this works in a biological system
is subtle and not obvious, so
let's consider a simpler example
(Fig. 1).
Suppose I have 8 boxes stacked up in a cube and you want to find the location of some candy which I put into one of them. You can ask me questions, but I will only answer with ``yes'' or ``no''. What is the minimum number of questions that you need to ask? There are poor ways to play this game, and the most obvious way to play it is not the best way. If you point to each box successively and ask ``is that it?'', you would require an average of 4 questions, since half of the time it would be in the first four boxes and the other half of the time it would be in the second four boxes. (Even if you knew that the candy was in the last box--because the first seven answers were ``no''--you would still ask the 8th question when using this method.) In contrast, information theory tells us that you only need
- 1.
- Is it in the left set of four boxes?
- 2.
- Is it in the upper set of four boxes?
- 3.
- Is it in the back set of four boxes?
Our challenge is to understand what the ribosome is doing
in terms of the choices made.
The problem is that
a ribosome doesn't work by cutting the genome in half
in a series of steps. Instead, it looks at
whole patterns in the RNA by physical touching.
Ribosome binding sites are like addresses, so let's label
our boxes in binary:
(See Fig. 2.)
If no = 0 and yes = 1, these correspond to the 8 possible answers to the questions listed above. We need three binary digits (i.e. bits) to label the 8 boxes. Notice how each question chooses a subset of four of the boxes in the figure. For example, if the first digit is 1, the box is one of the 4 on the left side.
Unlike a human,
a ribosome searches by random Brownian motion, and when
it comes to the right pattern, it binds and starts translation
(Fig. 3).
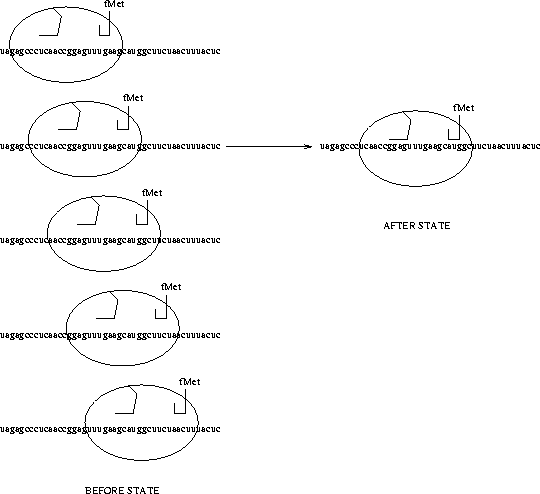
The messenger RNA which the ribosome is searching is shown as a string of a's, c's, g's and u's. This particular sequence is from the coat gene of the MS2 virus [Gold et al., 1981]. The ribosome is depicted as an ellipse with two hook-like pieces. The left one represents the 3' end of the 16s rRNA, which is the part of the ribosome which recognizes the Shine and Dalgarno sequence [Shine & Dalgarno, 1974], and the right one represents the first transfer RNA to which is attached a formylmethionine (fMet), the first amino acid of the new protein. On the left are shown a few of the states of the ribosome before it has found the start site, while on the right is the shown the state after the ribosome has found the Shine and Dalgarno (``ggag'') and the initiation codon (``aug''). |
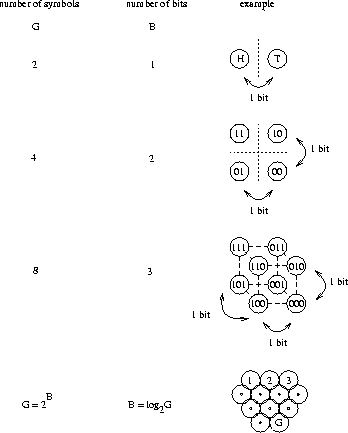
To model this, we have to change the game a little more: I present labeled boxes to you in an arbitrary order and you have to choose the one which has the candy in it. For example, we might agree beforehand that the label 010 means ``candy'', so you would look for a 010 pattern and when you see this you get to eat the candy inside the box. To make this system work, the proper number of bits has to be written on each box. Clearly 3 bits is the best solution, since 2 bits would be ambiguous and 4 bits would be wasteful.
Now suppose I hid two candies in two different boxes. We can take advantage
of the ambiguity when we set the system up. We drop the first question (bit)
from each element in list (1)
and label the 8 boxes as:
Candy is in both of the boxes labeled 10. As I randomly present boxes to you, you look for these bits. When you see them, you grab the box and open it for your snack.
You might object at this point, saying that you only need one bit to do the job: simply label the box that has candy 1 and put 0 on each empty box. To address this objection we will make the game even more realistic. Suppose that each box contains a different item, and we need all of these items at various times. Besides candy, there might be various tools, other kinds of food and so on. Because the boxes have various uses, they need full length labels to be distinguished. This does not mean we have to read the entire label in every case. For example, we could have a code which said that all boxes with food in them begin with 0. In the case of our candies, we can still label each box with 3 bits, but instead of dropping the first bit from the box, we simply ignore it in list (1).
The recognition model that we have made by this step wise process is subtly different from the divide-and-conquer model we began with. The reason we need it is that the ribosome must make choices, but it cannot do so by divide-and-conquer.
Now suppose I have
![]() boxes and have put 2600 candies in them.
How many bits do you need on each box to identify
those which contain candy?
This corresponds exactly to the problem the ribosome faces.
boxes and have put 2600 candies in them.
How many bits do you need on each box to identify
those which contain candy?
This corresponds exactly to the problem the ribosome faces.
For 8 boxes we needed 3 bits.
If we doubled the number of boxes to 16, we would need one more yes-no
question to find a particular box, so a total of 4 bits would be needed.
The number of boxes we can choose from, G, grows exponentially
as a function of the number of bits, B, according to
G = 2B (Fig. 2).
Rearranging this equation to
![]() we find that the number of bits required
grows by the logarithm to the base 2 of the number of boxes.
we find that the number of bits required
grows by the logarithm to the base 2 of the number of boxes.
Now, if 2 of these boxes contained the items you want, you could ignore
1 bit because you wouldn't need to make one decision.
If 4 of the boxes had what you want, you could ignore 2 bits;
with 8 items you could ignore 3 bits.
In this last case, you would get the candy from any box you choose,
and you could ignore the entire label.
In general, for ![]() boxes with items in them
you can ignore
boxes with items in them
you can ignore
![]() bits.
(
bits.
(![]() is the Greek letter ``gamma''.)
That is, you only need
to look at
is the Greek letter ``gamma''.)
That is, you only need
to look at
![]() bits. We call this number
Rfrequency for two reasons. First, it is
directly related to the rates, R,
of information transmission Shannon was thinking
about way back in the 1940's [Shannon, 1948,Shannon & Weaver, 1949]:
it is the average number of bits needed per candy (or binding site)
finding operation.
Secondly, by rearranging the equation
bits. We call this number
Rfrequency for two reasons. First, it is
directly related to the rates, R,
of information transmission Shannon was thinking
about way back in the 1940's [Shannon, 1948,Shannon & Weaver, 1949]:
it is the average number of bits needed per candy (or binding site)
finding operation.
Secondly, by rearranging the equation
as:
and we see that
For ribosomes,
![]() and
and
![]() so the
Rfrequency needed to locate the sites is 10.8bits per site. Keep this number in mind.
so the
Rfrequency needed to locate the sites is 10.8bits per site. Keep this number in mind.
Because we used an exact number of ribosome binding sites (as opposed to saying that some are stronger and others weaker for binding), we have implicitly assumed that these sites are distinct from all other positions on the genome. In Level 1 theory, we will justify this assumption.
Since Rfrequency depends on the number of sites and the size of the genome, it is fixed by the physiology and genetics of the organism. In contrast, the sequence patterns at the binding sites--corresponding to the labels on our boxes--could have any amount of information independently of Rfrequency. That is, Rfrequency is a prediction about how many bits are needed by the ribosomes to find their sites. Is there enough information at the sites to handle it?
Fortunately for us, many biologists have been busy figuring out the sequences of
genes in E. coli. In DNA, these
consist of long strings of A's, C's, G's and T's,
called ``bases'' or ``nucleotides''.
When a gene is turned on, an RNA copy of these strings is made
which differs from DNA in three ways:
first, instead of being a double helix, it has only one strand;
secondly
the sugar in the connecting backbone is ribose instead
of deoxyribose and finally ``U'' is used instead of ``T''.
Ribosomes start translating the RNA
at a pattern that has a cluster of G's and A's followed
by a gap, and then AUG but sometimes GUG or UUG.
In Fig. 4
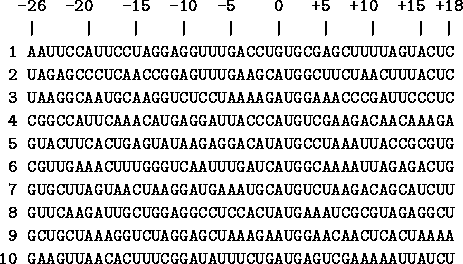
The coordinates are given above the sequences. Translation into protein starts at positions 0 through 2 and proceeds to the right. The sequences in this list are from [Gold et al., 1981,Stormo et al., 1982b]. |
we show several examples of ribosome binding sites. Notice that at the zero position there are mostly A's but one gene has a G, and that in positions +1 and +2 there are always U's and G's, as we said above. If you look closely you will see the G/A patch in the region around -10.
How much information do we need to describe the patterns here?
To say that position +1 always has a U requires telling you 2 bits
of information since that is a selection of one thing (U) from four
things (A, C, G, U).
If a position has half A and half G, then that is a selection of 2 from
4, or only 1 bit.
In the case of the ribosome we again apply the idea of before
and after states. Before binding, the ribosome's
``fingers'' see 4 possibilities and don't distinguish amongst them.
We say that each finger is ``uncertain'' by
![]() bits.
After binding, the uncertainty at each finger is lower.
If there is 1 base, then the uncertainty is
bits.
After binding, the uncertainty at each finger is lower.
If there is 1 base, then the uncertainty is
![]() bits.
The decrease in uncertainty is a measure of the sequence conservation or
information at the binding site. With 1 base this is
bits.
The decrease in uncertainty is a measure of the sequence conservation or
information at the binding site. With 1 base this is
![]() bits.
If a finger accepts 2 bases after then the uncertainty
remaining is
bits.
If a finger accepts 2 bases after then the uncertainty
remaining is
![]() bit and the information is
bit and the information is
![]() bit.
When a ``finger'' accepts all 4 bases, it really
doesn't do anything and the information it demands in sequence
conservation is
bit.
When a ``finger'' accepts all 4 bases, it really
doesn't do anything and the information it demands in sequence
conservation is
![]() bits.
When the frequencies are not 0, 50 or 100 percent,
a more complex formula is needed to calculate the uncertainty
after for each finger:
bits.
When the frequencies are not 0, 50 or 100 percent,
a more complex formula is needed to calculate the uncertainty
after for each finger:
where f(b, l) is the frequency of base bat position l. The derivation and use of the H formula been described in great detail elsewhere [Shannon, 1948,Pierce, 1980,,Schneider, 1988,Schneider & Stephens, 1990,,Shaner et al., 1993]. Using H(l), we can calculate the information at every position in the site according to:
where we have replaced
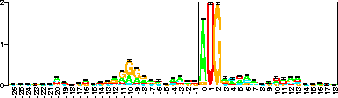
Sequence logo [Schneider & Stephens, 1990] for 149 E. coli ribosome binding sites. The vertical scale is in bits (the black bar is 2 bits high) and the horizontal scale is positions across the sites. Data are from [Schneider et al., 1986]. Error bars are for the height of the stack. Coordinates are the same as in Fig. 4. See the text for further details. |
which consists of several stacks of letters. The height of each stack is the information according to equation (6) while within the stack the relative heights of the letters are proportional to their frequencies in the binding site. Notice that the logo instantly shows the features of ribosome binding sites we described above along with many other details. The sequence logo represents the pattern of information, or label, used by the ribosome to indicate ``start translation here''.
The logarithm is used to calculate
information because this gives it a nice property: it is additive
if the information sources are independent.
We can calculate the total amount of pattern in ribosome
binding sites simply by summing the information from each position
given by equation (6):
This is the same as the area under the logo. We get:
The close proximity of Rsequence to Rfrequency has also been found in other genetic systems [Schneider et al., 1986,Schneider, 1988,Penotti, 1990]. There are also apparent exceptions, from which we are learning interesting biology [Schneider et al., 1986,Schneider & Stormo, 1989,,Stephens & Schneider, 1992,]. However, for this paper we want to ask: was it justified to make a model in which ribosome binding sites are completely distinct from everything else? Certainly the Rsequence/ Rfrequencydata support that model, and it makes good biological sense, but we can go back to Shannon's work to find a theorem which proves it is possible.
3. Level 1 Molecular Machine Theory: Channel Capacity and Precision
When we encounter a noisy phone line, we tend to shout to compensate.
This helps us to send more
information to the receiver. Likewise, a radio station which has been
assigned a restricted range of frequencies by the Federal Communications
Commission (in the USA) could use another slice of bandwidth to send more
news and entertainment.
To describe these relationships,
Shannon introduced the concept of channel capacity (C, bits per second).
This is a function of bandwidth (W, cycles per second),
signal power dissipated at the receiver
(P, joules per second) and thermal noise at the receiver
(N, joules per second)
according to the formula:
[Shannon, 1948,Shannon & Weaver, 1949]. P/N is the so-called signal-to-noise ratio. Shannon proved an amazing theorem about the channel capacity. The first part of the theorem says that if we want to send information at a rate R (bits per second) greater than the channel capacity, (R > C) we will fail, and at most the amount C will get through. Noise destroys the rest. (In the worst case, nothing will get through.) The second part of the theorem contains the surprise. If we send at a rate less than or equal to the capacity (
Our success so far in applying information theory to biology (i.e. Level 0) suggests that the channel capacity results should also apply, but to do this we must translate these ideas into biological terms. We will sketch this translation using the ribosome as an example. Please refer to [Schneider, 1991a] for a more rigorous derivation.
Biologists use the analogy of a lock and key to describe the precise interaction of an enzyme and its substrate [Gilbert & Greenberg, 1984]. Inside a conventional pin-tumbler lock there is a row of little metal cylinders called ``pins'' [Macaulay, 1988]. In the simplest kind of lock there are two pins, one on top of the other, at each position in the row. The pins can move up and down together in their slots. The combined length of each pair of pins is constant, but the division between them varies up and down. When the proper key is inserted, these divisions are all aligned at the ``shear line'' and the lower pins can be rotated away from the upper pins. This opens the lock. The wrong key allows one or more pins to prevent the turning. Notice that the pins have to move independently for the lock to work properly. Also, if two pins weren't independent then either the lock would never open, or it would be easier to pick it.
Now imagine that the surface of the ribosome has a series of ``pins''. A representation of the corresponding ``key'' is shown in Fig. 5. The model we are building says that:
(1) The pins of the ribosome are, to a first approximation, spread linearly along a groove into which the RNA fits.
(2) The pins move independently. (See [Schneider, 1991a] and [Stormo et al., 1982a] for evidence that this assumption of independence is reasonable.)
(3) Each of the three independent directions that a body can move in space corresponds to an independent pin.3
(4) Each pin can be modeled by a simple harmonic oscillator.
Thermal vibrations and collisions with neighboring molecules cause the pins to bounce around like weights on springs in the middle of a three-dimensional hailstorm. Most of the time a pin moves slowly, but on occasion it is hit hard by a neighboring molecule and moves quickly until it hits something else or recoils. The total velocity is the sum of many small impacts, so a series of independent velocity measurements would have a bell-shaped Gaussian distribution.
The velocity of an oscillating body in a vacuum
follows a simple sine wave, so it has both an amplitude
and a phase as independent degrees of freedom.
In polar coordinates, the amplitude is represented as the distance from
the origin, while the phase is represented by the angle.
In polar coordinates the phase and amplitude do not have the same units
of measure, but if we convert to
rectangular coordinates, we have two numbers which have the same units.
(They are actually the two Fourier components of the sine wave.)
These two numbers define a point on a plane.
If the oscillator is in a thermal bath it is frequently jostled, so
a moment later the x and y velocities are slightly different and
so the state of the oscillator is represented by a different point.
Surprisingly, the distribution of a large
collection of such points is circularly symmetric.4
Three independent descriptive numbers
(i.e. from
![]() pins)
define a point in a three dimensional ``velocity space'', and the
distribution of many such points
is spherical. This distribution
is known as the Maxwell gas distribution,
since molecules of gas have the same velocity distribution. With four numbers,
the distribution
becomes a four-dimensional sphere. As we add more pins, we need more numbers
to describe their velocities, and the distribution moves into
even higher dimensional
space. Fortunately the resulting distribution is easy to understand
because it is spherical, and its surface becomes more and
more distinct as the dimension increases.
This is because the total energy in
a large molecule fluctuates only a small amount, and
the sum of the squares of each velocity component
is proportional to the total energy.
The square root of
that sum is also the distance of each point from the origin
in velocity space, so the approximately constant
energy means that the points form a thin shell.
In really high
dimensions it looks like a ping-pong ball
in that it has a sharply defined surface.
In contrast,
each point defines a vector from the center of the space
whose direction
changes drastically from moment to moment.
Every point on this sphere represents an instantaneous configuration of
the pin velocities. In the next instant
the velocities will be similar, but slightly different so
a near-by point will be occupied. As a result,
the changing velocities trace a Brownian
motion path over the sphere surface,
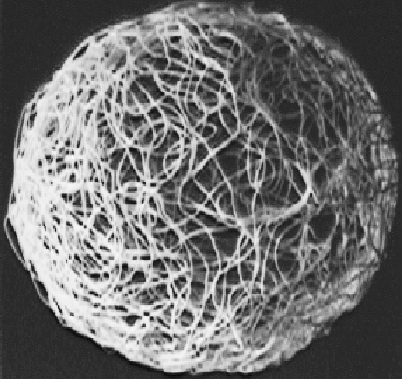
as represented by the squiggling string in
Fig. 6.
The sphere
has a radius proportional to the square root of the temperature,
so we can think of it as a ``thermal noise sphere''.
pins)
define a point in a three dimensional ``velocity space'', and the
distribution of many such points
is spherical. This distribution
is known as the Maxwell gas distribution,
since molecules of gas have the same velocity distribution. With four numbers,
the distribution
becomes a four-dimensional sphere. As we add more pins, we need more numbers
to describe their velocities, and the distribution moves into
even higher dimensional
space. Fortunately the resulting distribution is easy to understand
because it is spherical, and its surface becomes more and
more distinct as the dimension increases.
This is because the total energy in
a large molecule fluctuates only a small amount, and
the sum of the squares of each velocity component
is proportional to the total energy.
The square root of
that sum is also the distance of each point from the origin
in velocity space, so the approximately constant
energy means that the points form a thin shell.
In really high
dimensions it looks like a ping-pong ball
in that it has a sharply defined surface.
In contrast,
each point defines a vector from the center of the space
whose direction
changes drastically from moment to moment.
Every point on this sphere represents an instantaneous configuration of
the pin velocities. In the next instant
the velocities will be similar, but slightly different so
a near-by point will be occupied. As a result,
the changing velocities trace a Brownian
motion path over the sphere surface,
as represented by the squiggling string in
Fig. 6.
The sphere
has a radius proportional to the square root of the temperature,
so we can think of it as a ``thermal noise sphere''.
The sphere represents the set of all possible velocities of the pins of the ribosome while it is bound to the ribosome binding site waiting for the raw materials with which to begin translation. Therefore it represents the state of the ribosome after it has found the sites, and so we call it the after sphere. This corresponds to the after state shown in Fig. 3.
Recall that one of the ribosome's jobs is to find sites for initiating translation. Before it has done this it is anywhere on the RNA (Fig. 3). (In this model we set aside the problem of finding the RNA.) For the ribosome to stick to its sites, it must give up some energy to the surrounding medium. So before being bound to its sites, it must have more energy than after. At the moment the ribosome binds to its sites, the formation of non-covalent bonds converts this potential energy to kinetic energy which is almost immediately dissipated into the surrounding environment, since the ribosome has no way to hold on to it. (As a small molecule surrounded by a huge thermal bath, there is no way for the ribosome to be insulated from the surrounding salt and water medium and the ribosome's kinetic impacts on the surroundings will quickly transfer the excess kinetic energy away.) So before binding, the ribosome has a potential energy with which it could attain a higher velocity. Because this energy is released and dissipated during binding, before binding the ribosome is effectively in a larger sphere in the high dimensional velocity space. We call this the before sphere. This is a somewhat subtle concept because before binding the ribosome is at the same temperature as the surroundings and after binding it is also at equilibrium with the surroundings. Basically, the before sphere reflects the velocities the ribosome could obtain from the potential energy it carries before binding. In the same way, we speak of the potential energy of a ball sitting calmly on a table as being equal to the kinetic energy it would have at the moment it hits the floor after having rolled off the edge.
When the machine is in an after state,
it has energy from the thermal noise, Ny joules.
(The subscript y refers to the velocity space, which is
called Y-space.)
The energy of a mass is proportional to its
velocity squared, so
Ny = (rafter)2.
(We normalize to remove the proportionality constant.)
Turning this around, it means that the radius in velocity space
is related to the square root of the energy:
![]() .
In the before state the machine has additional energy
Py joules (which it will dissipate during the
machine operation), so the total energy before is Py + Ny.
That means that the radius of the before sphere is
.
In the before state the machine has additional energy
Py joules (which it will dissipate during the
machine operation), so the total energy before is Py + Ny.
That means that the radius of the before sphere is
![]() .
.
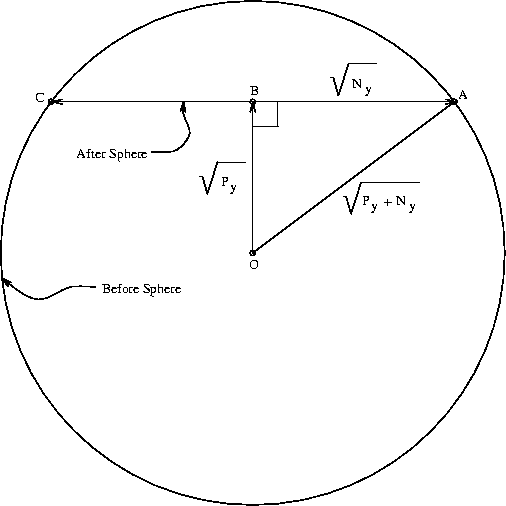
Consider a three-dimensional thermal-noise sphere. If we are in the center
of the sphere and move north, then there will be two dimensions
orthogonal to our direction of motion.
Noise can interfere with our motion in both of these directions.
In higher dimensions,
the geometry of this situation is both weird and interesting;
it is shown in Fig. 7.
Suppose we have a 100 dimensional space, and we move ``north''. Then 99% of the interfering noise is orthogonal to our motion. The molecular machine operation can be thought of as the collapse of the before sphere with the concomitant movement of the sphere center from point O to B. Since 99% of the noise is at right angles to the line segment between 0 and B, the after sphere can be represented by the straight line segment running from C to A. As the dimensionality increases, we may neglect the small amount of noise in the direction O to B. The after sphere is still spherical, but must be represented in this diagram by a straight line segment. Weird! Now, we know that the before sphere has a radius of
The molecular operation that the ribosome must perform is to
select the after sphere that represents its binding sites and to avoid
all the other after spheres that represent different patterns.
As we showed above,
the before sphere encloses all of the after spheres [Schneider, 1991a].
How many choices can the ribosome make for a given energy dissipation?
In other words, how many after spheres can fit into the before
sphere?
A gumball machine is a good model for the situation
(Fig. 8).
We can calculate an upper bound for this simply by dividing the volume of the before sphere by that of an after sphere.
A circle has an area of ![]() ,
while the volume of a sphere
in three dimensions is
,
while the volume of a sphere
in three dimensions is
![]() .
In a higher
dimension, D,
the volume is proportional to rD.
Thus the volume of the before sphere is
.
In a higher
dimension, D,
the volume is proportional to rD.
Thus the volume of the before sphere is
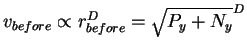 and that of the after sphere is
and that of the after sphere is
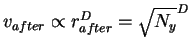 .
The maximum number of small after spheres which can fit
into the larger before is therefore
.
The maximum number of small after spheres which can fit
into the larger before is therefore
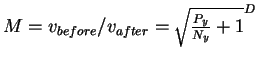 .
.
For every pin of the molecule, there are two degrees of
freedom of movement (the phase and amplitude projected onto
the x and y axes, as mentioned earlier), so
the dimensionality
D = 2 dspace, where dspace is the number of pins.
With this we find
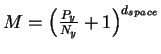 .
.
The base 2 logarithm of the maximum number of choices made
is the capacity Cy (in bits), since it represents
the largest number of distinct
binary decisions the machine could make for the given
energy dissipation Py. To calculate this
we take
![]() ,
and find the molecular machine capacity:
,
and find the molecular machine capacity:
dspace is the number of pins, Py (joules per operation) is the energy the machine has to give up to go from before to after and Ny is the thermal noise (in joules) which defines the after sphere radius. Notice the resemblance to equation (8). Notice also that the information measures Rfrequency, Rsequence and Cyare all different views of the same before to after state change. Because we use the same sphere geometry that Shannon did (see Appendix 2 of [Schneider, 1991a]), we can immediately apply his theorem, which he proved geometrically [Shannon, 1949]. When translated into molecular biology and applied to ribosomes, the theorem says:
As long as the ribosome operates at or below its machine capacity, it can be as precise as is necessary for survival.
This theorem shows that it is possible for ribosomes to almost completely avoid making the wrong proteins but to still pick out all the right ones. To what degree they do this will depend on the evolutionary ``pressures'' the organism faces. The price that must be paid to obtain this result is that the ribosome must work in a high dimensional space so that the spheres have sharp edges. In other words, the ribosome is forced to have many energetically tiny contacts. This makes ribosome binding sites distinct from other sequences. Since the independent pins of the ribosome appear to be strung out along the RNA, it seems that all those subtle bumps in the sequence logo (Fig. 5) are clues to the code the ribosomes must be using to choose sites.
Notice how messy the ribosome binding site patterns seem to be in Fig. 4 and Fig. 5. This has led people to think that ribosomes could not possibly locate the sites precisely. However, the theory says that the more tiny contacts exist, the more precise the ribosome could become. So the apparent messiness could be, paradoxically, helping the ribosome to be precise!
4. Level 2 Molecular Machine Theory: The New Maxwellian Demons
In 1867, James Clerk Maxwell introduced to the world
a little being with a fine touch
and a propensity for trouble [Maxwell, 1904].
This demon controls a door between two gas vessels,
and
he uses the door to
sort molecules (Fig. 9).
When a rapidly moving molecule approachs from the left, he lets it through, but a slow one is not allowed passage. Fast ones from the right don't pass him but slow ones from there do. In this way, fast molecules end up in the right hand container, which becomes hotter, and slow molecules go to the left, which becomes colder. The temperature difference could run a steam engine and supply the world with free energy. The demon is not creating energy from nothing, which would be a First Law violation. Instead, he is violating the Second Law by decreasing the entropy of the system (by doing the separation) without compensatory heat dissipation. Although the demon does nothing more than open and close a door, it seems that one could get a perpetual motion machine that violates the Second Law of Thermodynamics. One of the many forms of this fundamental law [Jaynes, 1988,Atkins, 1984] states that it is not possible to move heat from a body at a lower temperature to one at a higher temperature without performing work. Since it has not been clear what kind of work the demon performs, he has been causing consternation ever since [Leff & Rex, 1990].
To see the gas molecule, Brillouin supplied the demon with an ``electric torch'' [Brillouin, 1951]. Clearly most of the photons won't bounce off the gas molecules and they would change the energy of the molecules if they did (from the Heisenberg uncertainty principle). Worse, not all of those few that manage to come back to the eye of the demon will be absorbed. For some reason, these and other serious difficulties are usually ignored in the literature, perhaps because the demon is not thought of as being composed of molecules. The Maxwell demon problem is real, but making absurd assumptions only clouds the issues. For example if we assume that there is no thermal noise, as physicists sometimes have, then the machine's capacity goes to infinity according to equation (9). We will try to stick to realistic physics and biology.
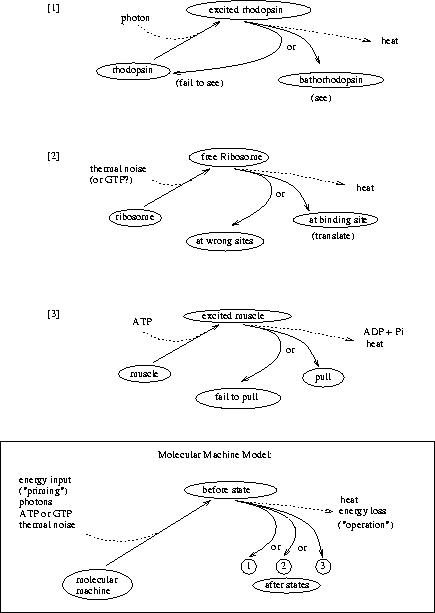
What is the demon doing? Let's split the problem into
its components. As each molecule approaches he must [1] see it, then
he must [2] decide what to do, and finally he must [3] operate the
door accordingly. All three of these molecular operations dissipate
energy, and they correspond to actions of
the molecules of [1] rhodopsin, [2] genetic control
elements like the ribosome and EcoRI and
[3] muscle. These molecular machines all choose substates from
several possibilities so they fit the
theory described here (Fig. 10).
[1] If it can see,
the demon must have rhodopsin (or a rhodopsin-like molecule) because
otherwise it is unrealistic.
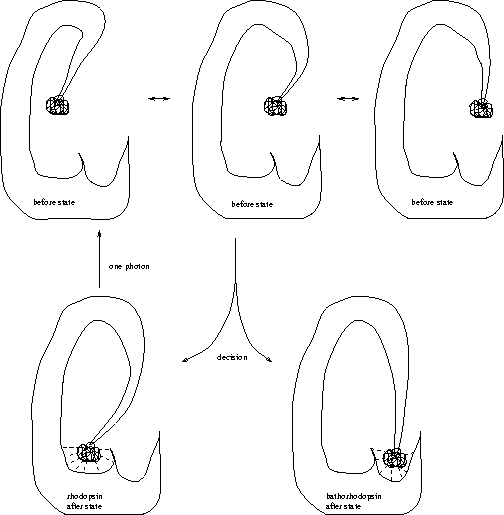
An excited molecule of rhodopsin can flip into a state called
bathorhodopsin (Fig. 11).
In vertebrate eyes, once a single bathorhodopsin has formed it triggers 400,000 chemical reactions, which then cause a nerve impulse. For this reason, we can see single photons [Lewis & Priore, 1988]. All this happens at room temperature, so the molecule operates in the presence of thermal noise. The energy of the photon must be dissipated for the molecule to choose between bathorhodopsin and the original unexcited state, just as a ribosome must dissipate energy to bind to its binding site. Thus rhodopsin is a molecular machine that makes decisions.
[2] The brain of the demon must decide what to do. Ribosomes are an example of genetic control elements which make decisions by choosing their binding sites from among other sequences in the genome.
[3] The same must be true for muscle, in which myosin heads ``walk'' along actin fibers. Each myosin head must dissipate energy derived from a broken energy molecule--ATP--to choose between its original state and one step forward.
Thus all the demon's actions--seeing, computing and movement--require decisions to be made by molecular machines. The fundamental question now is: does making decisions require using energy?5 If so, the demon must be given energy to do its job, and the problem is solved.
Surprisingly, the solution comes from the molecular machine capacity
formula (9).
Cy has units of bits per molecular machine operation.
The power Py has units of joules (dissipated from the machine into
the surroundings) per molecular machine operation.
Thus we can define a new variable, the energetic cost:
which has units of joules per bit, just the right ones to answer the question. Now, what happens to
where we have substituted first from equation (10) then from equation (9) and converted to the natural logarithm in preparation for the next step. L'Hôpital's rule [Thomas, 1968] tells us to take the derivative of both top and bottom and try the limit again:
Because we don't know values for dspace and Ny, we appear to have reached an impasse, but this is not so. Nyquist showed in 1928 that there is a simple formula for thermal noise [Nyquist, 1928]. For every independent degree of freedom in a system, the thermal noise is
Because the pins in a molecular machine move independently,
we can model each of them
as a simple harmonic
oscillator surrounded by a thermal bath,
as we did earlier to construct the thermal noise sphere.
Since each oscillating pin has a phase and an amplitude,
it has two degrees of freedom.
(Note: the phase and amplitude change with time because
the oscillator is being bombarded by the surrounding molecules.)
Since there are dspace independent pins in the machine (by definition),
and the number of degrees of freedom is twice this,
we can calculate the thermal noise from:
Substituting this into (13) gives
In electrical engineering
power is given in joules per second, so it may approach
zero as the energy decreases or as the time taken for dissipation
increases.
Neither approach alters
equation (13),
so it is incorrect to think that the limit
![]() can be bypassed
by slowing the energy dissipation
of a device such as a computer. In the case of individual molecules
operating at a certain (perhaps irregular) rate per second,
the power is given in joules per molecular operation.
That is, the energy to be dissipated is the same as the power
during one operation and time is irrelevant because we only count
complete operations.
can be bypassed
by slowing the energy dissipation
of a device such as a computer. In the case of individual molecules
operating at a certain (perhaps irregular) rate per second,
the power is given in joules per molecular operation.
That is, the energy to be dissipated is the same as the power
during one operation and time is irrelevant because we only count
complete operations.
Now we start an entirely different approach.
To do this it is first important to clarify the relationship between
information and entropy. Shannon's information measure is based
on the concept of uncertainty
[Shannon, 1948].
The more possible distinct
states that a system has, the higher the uncertainty.
Since Shannon required additivity, he found that the uncertainty
should be the logarithm of the number of possible states.
If the possible states are not equally likely, the formula is:
where Pi is the probability of the
If I am sending you a series of characters, you will be uncertain
as to what character I will send next before you receive
each character. After receipt, your uncertainty is
lower, but not necessarily zero. If there is noise of some kind,
it will not affect your uncertainty before receipt, but will
affect your uncertainty after.
More noise means that less information gets through.
Thus the decrease in uncertainty
that a communications receiver experiences is
the information that the receiver gains.
Information is always measured as a state
function difference.
Likewise,
the decrease in uncertainty that a molecular machine
experiences is the information that the machine gains. That is,
where R is the information gain. `R' stands for the `rate' of information gain, in this case per operation. If there are a given number of operations per second, one can convert to bits per second.
Entropy is another state-function measure of a system.
The Boltzmann-Gibbs entropy of a physical system,
such as a molecular machine, is
where
any microstates which are not accounted for that do not alter between the two states will cancel. For example, the information needed to choose one thing in two is the same as the information needed to choose two things from four because the extra factor drops out during the subtraction of the logarithms. This solves the problem of relating information theory to thermodynamics, which many writers have complained is not possible. See [Schneider, 1991b] for further discussion.
Combining equation
(16)
with
(18)
and substituting into
(17)
and
(19)
gives:
This shows that, under the condition that the probabilities refer to the same microscopic states--which is a reasonable assumption in the case of molecular machines--a decrease in the entropy of the molecular machine corresponds to an increase in the information of that machine. In other words, for a molecular machine to make choices, its entropy must decrease.6
Now we are ready to start the second approach to
the question of information versus energy use
in a molecular machine.
It is well known
that the Second Law of Thermodynamics can be
expressed by this equation:
where dS is the entropy increase of a system corresponding to dq, the heat flowing into the system at temperature T[Tolman, 1938,Fermi, 1936,Jaynes, 1988]. The system in this case is a molecular machine, and the surrounding is the huge thermal bath of the cell or fluid the machine is in. As we discussed earlier, the molecular machine is completely exposed to the solvent, so its temperature before is the same as after the operation. Because the temperature is a constant, we can integrate and rearrange:
(where
If we set R = 1, this formula says that for every bit of information gained, the heat dissipated into the surroundings (i.e. negative q) must be more than
Let us define the energetic cost as the heat given up
for the information gained:
so that equation (23) becomes:
The smallest possible value of
Surprise! This is the same formula we derived from the channel capacity, equation (15)! Since we took a limit to obtain this, the channel capacity is a more general law than the Second Law under isothermal conditions.8
Because the capacity formula gives a precise bound
according to Shannon's theorem,
we can see that
![]() also defines a precise limitation on the capabilities
of a molecular machine.
Equations (15) and (26) say that for
every bit of decision Maxwell's demon makes, it must dissipate at least
also defines a precise limitation on the capabilities
of a molecular machine.
Equations (15) and (26) say that for
every bit of decision Maxwell's demon makes, it must dissipate at least
![]() joules of energy into the surrounding environment.
It can dissipate more, but it cannot dissipate less, since
to do so would violate both Shannon's channel capacity
theorem and the Second Law.
To preserve the First Law,
the energy used to prime the machine into its before state
must come from somewhere else,
so the demon must use at least
joules of energy into the surrounding environment.
It can dissipate more, but it cannot dissipate less, since
to do so would violate both Shannon's channel capacity
theorem and the Second Law.
To preserve the First Law,
the energy used to prime the machine into its before state
must come from somewhere else,
so the demon must use at least
![]() joules to see the gas molecule,
another
joules to see the gas molecule,
another
![]() joules to
decide which kind of molecule it is,
and another
joules to
decide which kind of molecule it is,
and another
![]() joules to
choose the proper door configuration.9
We might imagine then that if the demon only passes molecules
with energy more than
joules to
choose the proper door configuration.9
We might imagine then that if the demon only passes molecules
with energy more than
![]() joules
then there would be a net gain in energy.
But a molecule with
joules
then there would be a net gain in energy.
But a molecule with
![]() joules of energy above background will be more rare
than one with less energy. In a thermal bath at equilibrium
(which is the situation the Demon starts with, and is a
better condition than the situation later on after he has been
working for awhile), the molecules follow a Boltzmann distribution
in which the probability p of a molecule with energy
joules of energy above background will be more rare
than one with less energy. In a thermal bath at equilibrium
(which is the situation the Demon starts with, and is a
better condition than the situation later on after he has been
working for awhile), the molecules follow a Boltzmann distribution
in which the probability p of a molecule with energy ![]() above background is
above background is
Letting
Another possibility is a ``pressure'' demon who captures molecules
from one side of a membrane and puts them on the other.
Such pumps are found on the surface of all cells, and
they use ATP to do their work.
Once the molecule is captured, this demon must decide
which side to put it on. This 1 bit decision costs at least
![]() joules of energy. The result is the evacuation
of one chamber and the filling of the other,
so the pressure difference could run an engine.
Classical thermodynamics tells us that if we allow the molecules
to spread out again
by expanding the volume of a piston,
the most work we could do with them
is
joules of energy. The result is the evacuation
of one chamber and the filling of the other,
so the pressure difference could run an engine.
Classical thermodynamics tells us that if we allow the molecules
to spread out again
by expanding the volume of a piston,
the most work we could do with them
is
![]() multiplied by the logarithm
of the ratio of the volumes
before and after. For doubling the volume
(a 1 bit loss in the positional uncertainty of the gas molecules),
the formula is
multiplied by the logarithm
of the ratio of the volumes
before and after. For doubling the volume
(a 1 bit loss in the positional uncertainty of the gas molecules),
the formula is
![]() ,
which is, of course,
,
which is, of course,
![]() ,
so this kind of demon can't win either.
,
so this kind of demon can't win either.
The problem with Maxwell's demon has been that he is imaginary, so it is easy to forget an important influence on his performance, such as thermal noise. By making our model of the demon match molecular machines found in cells, we can avoid this difficulty. To do this, we have split the operations of the demon into three simpler steps well known in biology: seeing, thinking and moving. For clarity, we further divided each of these steps into priming and choosing (Fig. 10). Having dissected the little bugger, let's see if he's still alive.
The Second Law was formulated because nobody could find a way around its various constraints on heat and work. No known violations exist, even at the molecular level [McClare, 1971]. Some people think that molecules can somehow bypass the Second Law because they are so small. If thermodynamics and statistical mechanics don't apply to molecular machines, then a single molecule could violate the Second Law of Thermodynamics. If one machine can violate it, then so could a large number of them acting in parallel. It is clear that this is not happening since living things depend heavily on the operations of molecular machines, yet they all need to eat energy molecules or photons.
The main question arising from Maxwell's demon
is whether the Second Law of thermodynamics
can be violated by some kind of subtle sorting operation.
The new form of the Second Law given by equation (26)
shows that for every bit of sorting
that the demon performs, he must pay at least
![]() joules
of energy dissipation away from himself.
He cannot win because that separation costs at least as much
as it would be worth, as shown above.
Thus the demon cannot violate the Second Law by doing
sorting operations. But sorting is the only trick that
the demon has available to him!
The demon violates the Second Law by decreasing
the entropy of a system without compensatory dissipation.
Maxwell's demon is dead.
joules
of energy dissipation away from himself.
He cannot win because that separation costs at least as much
as it would be worth, as shown above.
Thus the demon cannot violate the Second Law by doing
sorting operations. But sorting is the only trick that
the demon has available to him!
The demon violates the Second Law by decreasing
the entropy of a system without compensatory dissipation.
Maxwell's demon is dead.
The elimination of the demon from our discussion of these issues will not be a tragic loss. The demon has been like the proverbial angels-on-a-pinhead in that no two people agree on how to define the issues involved. This has led to a huge and confused literature [Leff & Rex, 1990]. We can clarify the problem of molecular sorting by replacing the imaginary demon with examples of real molecular machines. These biologically active molecules have the wonderful advantage that we can play with them in the laboratory to see if our models are reasonable [Schneider & Stormo, 1989].
5. Molecular Computers
The most important requirement for building a computer is a way to perform Boolean logic, since this allows one to construct logic circuits. Many molecules perform the AND function. For example, the EcoRI enzyme effectively asks whether
(base #1 is G) AND (base #2 is A) AND (base #3 is A) AND
(base #4 is T) AND (base #5 is T) AND (base #6 is C)
Genetic control systems often work by one molecule binding to a spot to prevent another molecule from binding there. This is a NOT operation. AND followed by NOT is a NAND, and all logical circuits can be constructed from NAND [Wait, 1967,Gersting, 1986,Schilling et al., 1989]. The theory of molecular machines shows that molecular machines can act as precisely as we choose, so nearly ideal Boolean logic could exist and complete molecular circuits should be possible to build. Thus we already know enough about molecular biology to know that molecular computers are possible.
These machines would have to dissipate at least the quantity of energy required by the Second Law of Thermodynamics, as given by equation (15). Fortunately this is only a tiny quantity compared to today's computers [Keyes, 1988], so molecular computers should be compact and energy efficient.
One of the confusing issues here is that the dissipation of a computer
need not be correlated to the number of Boolean operations we write
down. (See [Leff & Rex, 1990] for a review of ``non-dissipative'' computing,
and [Gonick, 1991a] for an introduction to circuit analysis.)
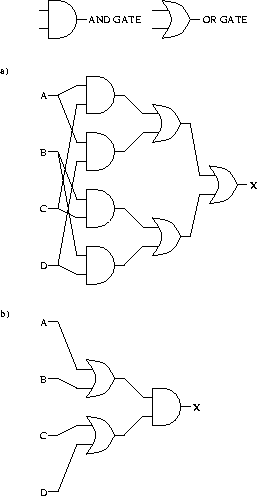
Following the convention that ![]() means AND, and that + means OR,
we can create a circuit with 4 inputs and 1 output
from the equation
means AND, and that + means OR,
we can create a circuit with 4 inputs and 1 output
from the equation
as shown in Fig. 12a.
Each of the 7 gates makes a choice between 0 and 1, so the total energy dissipation of the circuit as drawn would be at least
The equivalent circuit uses only 3 gates as shown in Fig. 12b, so this circuit would dissipate only
We can do even better than this. What really counts is the number
of choices the circuit makes [Feynman, 1987], its ``output''.
Since Boolean variable X has only two possibilities,
setting it must dissipate at least
![]() joules.
As Feynman pointed out, we can't avoid this dissipation.
joules.
As Feynman pointed out, we can't avoid this dissipation.
But there is an additional cost which Feynman did not identify.
Setting the input states A, B, C and Dtakes another
![]() joules no matter what the circuit is.
So the total minimum dissipation cost is
joules no matter what the circuit is.
So the total minimum dissipation cost is
![]() joules because
we have to count both the total number of inputs and
outputs
to find the cost of the operation.10
This is the lower limit for this circuit according to the Second Law.
Such a circuit
could operate like a key in a lock, with all computations being
done in one single concerted step.
joules because
we have to count both the total number of inputs and
outputs
to find the cost of the operation.10
This is the lower limit for this circuit according to the Second Law.
Such a circuit
could operate like a key in a lock, with all computations being
done in one single concerted step.
The discussions in the literature point out that we can perform arbitrary amounts of ``computation'' for little energy dissipation. There are two ways to see that this is both true and not necessarily as great as it sounds. First, ribosomes must ``compute'' the fact that they are not at a binding site, and since they don't stick in this case, they don't dissipate energy. Thus if we put a ribosome with some RNA that does not have a ribosome binding site, it would ``compute'' forever, with no dissipation at all. Of course it would never get to translate, so this situation is not profitable for a cell. The second way to see that huge amounts of computation are not necessarily so good is to notice that this seems to imply that it would be better to build the more complex circuit shown in Fig. 12a, which computes 7 boolean operations, rather than the equivalent simple one shown in Fig. 12b, which computes 3 boolean operations. That would, of course, waste building materials. Even larger amounts of computation could be had for even larger and more absurd circuits. The idea that infinite amounts of computation can be performed without any dissipation costs is therefore correct, but performing such extra computations (while keeping the same input and output) is just wheel spinning. The fundamentally required energetic cost is at the input and output of a computation. Memory must also choose states, so it too entails this cost.
Can we perform dissipationless computation? Surprisingly, this is done all the time in molecular biology labs around the world. We call them ``Southerns'', ``Northerns'', ``Westerns'' and even ``Far Easterns''.11 To perform a Southern, a molecular biologist will purify some DNA (from, for example, a person) then cut the DNA with a restriction enzyme such as EcoRI, which cuts between the G and A of the DNA sequence GAATTC. In the test tube there are many copies of the genetic material, and the enzyme chops up each piece at exactly the same places. This mixture is then put onto one end of gel, which is like a big slab of jello between two sheets of glass. A voltage applied to the gel forces the DNA to run between the sheets. Little pieces of DNA zip through fastest, while bigger pieces get tangled up in the gel and take longer. As a result, the EcoRI fragments separate by size inside the gel. Before the pieces run off the end, the gel is then removed and placed on top of some filter paper. The filter paper is put on top of some dry paper towels. Wet paper towels are put on top of the gel. Water runs through the gel and is absorbed in the dry towels. This transfers the DNA from the gel to the filter paper. The filter is removed and then baked to fix the DNA onto it. Next, a single piece of DNA called a ``probe'' is made radioactive. This is put in a plastic bag with the filter and some buffer. The probe is everywhere in the bag, but it will stick only to the DNA molecules on the filter to which it is complementary. (A pairs to T and C pairs to G.) The filter is washed and placed against film. Wherever the probe can pair to the filter-bound DNA, a black band appears on the film. In this way one can, for example, pick out single genes from the entire genetic material.
Inside the bag, each probe DNA tumbles in solution ``computing'' whether or not to bind to the genetic DNA. Only when it binds does a dissipation occur. Thus fixing the output of the ``Southern'' computer required dissipation. When the probe DNA was made, its sequence (choice of the order of the letters A, C, G, T) was determined. Making this choice required an energy dissipation. That is, setting the input to the ``Southern'' computer also requires energy dissipation. ``Westerns'' use the same idea, but the radioactive probe is an antibody, and the material spread out by size is a set of proteins. ``Northerns'' use RNA spread instead of DNA, and ``Far Easterns'' use a dried gel instead of a transfer to filter paper. Only the input and output of these methods dissipates energy, the ``computation'' itself doesn't.
Imagine a futuristic technology in which we had a molecule with a series of switches on its surface. We set the state of the molecule, dissipating energy to do so. We then release it on one end of a reaction chamber. The molecule then diffuses randomly by Brownian motion to the other side of the chamber where there is a bank of many kinds of receptors, each one representing a possible answer to the computation we are trying to perform. If the switch states of the released molecule match the surface of receptor, then the molecule binds and triggers an ``answer''. The entire computation is performed in a single concerted step. Input and output require energy dissipation, but the computation in between is ``dissipationless''. Such an advanced molecular computer is actually not so far fetched! We have just described a process similar to the hormonal communications in our bodies.
But how can we build molecular computers? Molecular biology allows us to construct any protein we can write down on paper. If we could build and connect together NAND gates, we could construct entire molecular computers. The reason we don't have them yet is that we don't know how to design proteins to fold properly, to bind to specific surfaces, or to use energy.
Fortunately, in the past few years a path to the construction of molecular computers has opened:
- 1.
- Stolen Parts. Modern molecular biology allows us to take pieces from nature and to hack together logic circuits like those in genetic control systems. This can be done now!
- 2.
- Evolved Parts. Powerful evolutionary techniques such as SELEX [Tuerk & Gold, 1990] and the creation of viruses which present variants of binding proteins on their surfaces [Smith, 1985,Scott & Smith, 1990,Delvin et al., 1990] should allow us to select the interacting surfaces we need to put molecular parts together or to construct logic circuits. But because these evolutionary methods work by guesses, and optimal solutions may be rare, this may be an arduous task.
- 3.
- Designed Parts. Because different codes correspond to packing the spheres together in different ways, the theory of molecular machines shows that the way to make molecules select their substates correctly is to code their structure properly. A long term challenge is to understand the coding used by molecular machines deeply enough that we can design them ourselves. The so-called ``genetic code'' is only one of many, since every molecular machine operation must involve a coded interaction, and there are many kinds of molecular machines in the world. Using the tools of molecular biology, we may choose to study any of these. Fortunately we already have 40 years of experience with coding theory [Sloane, 1984]. Once we have broken the codes of natural molecular machines, we will have opened the door to a fully engineered nanotechnology.
Acknowledgments
I thank John Spouge,
Mark Shaner,
Mort Schultz,
Peter Lemkin,
Stanley Brown,
Denise Rubens,
Jake Maizel
and
Paul Hengen
for useful conversations and
for comments on the manuscript;
April Cruz for the method of creating
Fig. 6;
Janice Currens, Jon Summers and Annie Chaltain for photography;
and
Linda Engle for her drawing of Maxwell's Demon.
Next: Bibliography Tom Schneider
2000-10-21