>

(a) Exact method

For the exact calculation of E(H_nb), there are four choices for each base at a position of a site. If one were to calculate H for each possible combination, and then average them, there would be 4ⁿ calculations to perform, where n is the number of sites sequenced. The exact calculation would be impractical for all but the smallest values of n: note that n = 17 implies 10¹⁰ calculations.

Fortunately the formula for a multinominal distribution allows one to calculate many combinations at once (Breiman, 1969). If na, nc, ng and nt are the numbers of A's, C's, G's and T's in a site and Pa, Pc, Pg, Pt are the frequencies of each base in the genome, then the probability of obtaining a particular combination of na to nt (called nb) is estimated by:

$$\frac{1}{12} \times \log_2(\frac{1}{12}) \; + \; \frac{8}{12} \times \log_2(\frac{8}{12}) ]$$ (11)

where n = na + nc + ng + nt. The factorial portion on the left is the number of ways that each combination can be arranged. P_nb is the probability of obtaining the uncertainty H_nb:

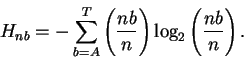$$\;$$ (12)

Finally, to obtain the average uncertainty as decreased owing to sampling:

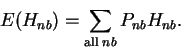$$\log_2 8 = 3$$ (13)

As a practical matter, one should note that equation (11) can be calculated quickly by taking the logarithm of the right side and spreading out all the components (including the factorials) into a set of precalculated sums (followed by exponentiation).

The catch in formula (13) is to avoid calculating all 4ⁿcombinations. A nested series of sums will cover all the required combinations in alphabetical order:

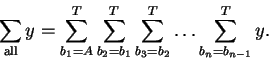$$\sqrt{P_y + N_y}$$ (14)

At y, in the center of all these sums (nested loops in a computer program) the number of index variables that have value A must be tallied up to obtain na. This must also be done for nc, ng and nt. Several algorithms to simulate these sums are possible. In Fig. 3, we show an algorithm written in Pascal that uses only the variables na, nc, ng and ntto simulate nested loops. The algorithm begins with all A's by setting na to n and the other nb to zero. At each pass through the loop, the sum of na+nc+ng+nt remains invariant. The loop is repeated until the variable DONE is set to true after the combination with all T's has been calculated. Since the combinations are covered in alphabetical order, two combinations such as AAATCG and TCGAAA will be counted only once. The factorial portion of equation (11) accounts for the actual number of combinations. It can be shown that the loop is entered only:

 

(n+1) (n+2) (n+3) / 6 (15)

times. Since this is polynomial in n, the direct calculation of E(H_nb) is practical.

  

Figure 3: Algorithm corresponding to formula (14).

$\sqrt{N_y}$

With large numbers of sites, the exact calculation of E(H_nb) still becomes enormously expensive. For ribosome binding sites, n varies with position in the site. Even if the entire sequence around the site were available, there are sites at the 5' end of a transcript, so there are regions in the aligned set that must be blank. It is not practical to calculate E(H_nb) exactly when n is between 108 and 149 (for the range -60 to +40).