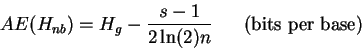>

(b) Approximate method

The second method to calculate the sampling error correction is from Miller (1955) and Basharin (1959) who derived an approximation for the expectation of a sampled uncertainty, AE(H_nb), that is good for large n:

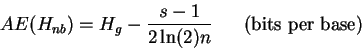$$\sqrt{P_y}$$ (16)

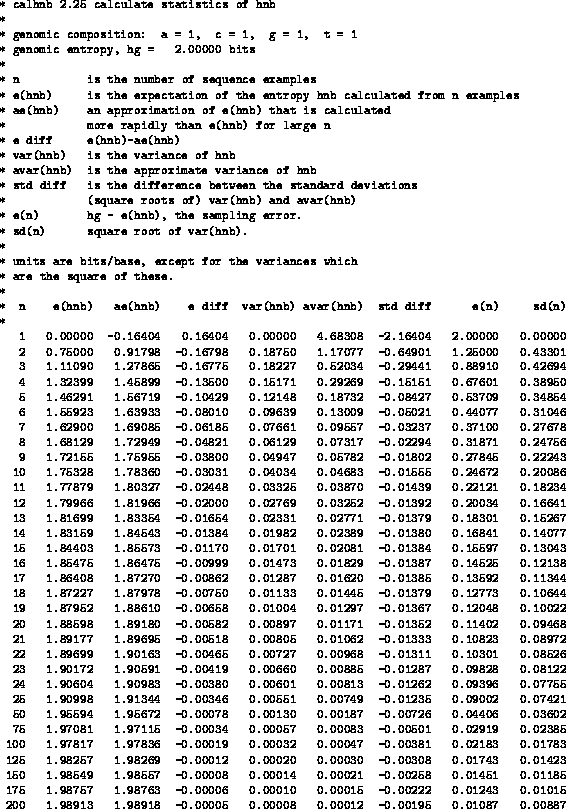
where s, the number of symbols, is 4 for mononucleotides. Fig. 4 shows E(H_nb) and AE(H_nb) for several values of n. This table⁹ helps one to choose between AE(H_nb)(a computationally cheap estimate that is inaccurate for small n but accurate for large n) and E(H_nb) (an exact calculation that is computationally costly for large n). We use AE(H_nb) above n=50 because the cumulative difference between E(H_nb) and AE(H_nb)in a site 100 positions wide would be at most 0.078 bits. The exact E(H_nb) is used for n less than or equal to 50 since its computation is rapid in this range.

  

Figure 4: Statistics of H_nb for equiprobable genomic composition.

$\lambda$