absolute coordinate: A number (usually integer)
that describes a specific position on a nucleic acid or protein sequence.
An example of using two absolute coordinates in
Delila instructions is:
get from 1 to 6;
The numerals
1
and
6
are absolute coordinates.
See also:
relative coordinate.
acceptor splice site:
The binding site of the spliceosome
on the 3' side of an intron and the 5' side of an exon.
This term is preferred over "3' site" because there can
be multiple acceptor sites, in which case "3' site" is
ambiguous.
Also, one would have to refer to the 3' site on the 5' side
of an exon, which is confusing.
Mechanistically, an acceptor site defines the beginning of the exon,
not the other way around.
See
acronymology:
The study of words (as radar, snafu) formed from the initial letter or letters of
each of the successive parts or major parts of a compound term.
administrivia:
[Pronunciation: combine administ[ration] and trivia.
Function: noun.
Etymology: coined by TD Schneider.
Date: before 2000]
administritrative trivia
after state (after sphere, after):
the low energy state of a
molecular machine
after it has made a choice while dissipating energy.
This corresponds to the state of a receiver
in a communications system after it has selected
a symbol from
the incoming
message
while
dissipating the energy of the message symbol.
The state can be represented as a sphere in a high dimensional space.
See also:
Shannon sphere,
gumball machine,
channel capacity.
alignment (align):
a set of
binding site
or protein sequences can be brought into register so that
a biological feature of interest is emphasized.
A good criterion for finding an alignment is to
maximize the
information
content of the set.
This can be done for nucleic acid sequences by using the
malign
program.
See also:
before state (before sphere, before):
the high energy state of a
molecular machine
before it makes a choice.
This corresponds to the state of a receiver
in a communications system before it has selected
a symbol from
the incoming
message.
The state can be represented as a sphere in a high dimensional space.
See also:
Shannon sphere,
gumball machine,
channel capacity.
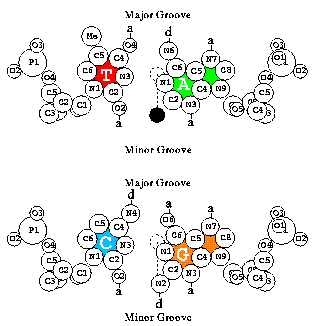
binding site:
the place
on a molecule
that a
recognizer
(protein
or macromolecular complex) binds.
In this glossary,
we will usually consider nucleic acid binding sites.
A classic example is the set of
binding sites for the bacteriophage Lambda Repressor (cI) protein on DNA
(M. Ptashne,
How eukaryotic transcriptional activators work,
Nature, 335, 683-689, 1988).
These happen to be the same as the binding sites for the Lambda cro protein.
(The text mentioned in the figure is Sequence Logos: A Powerful
Yet Simple, Tool.)
See also
binding site symmetry:
binding sites
on nucleic acids have three kinds
of asymmetry and symmetry:
- asymmetric - All sites on RNA and probably
most if not all sites on DNA bound by a single polypeptide will
be asymmetric.
Example:
RNA: splice sites;
DNA:
T7 RNA polymerase binding sites.
-
symmetric -
Sites on DNA bound by a dimeric
protein usually (there are exceptions!) have a two-fold dyad
axis of symmetry. This means that there is a line passing through
the DNA, perpendicular to its long axis, about which a 180 degree rotation
will bring the DNA helix phosphates back into register with their
original positions. There are two places that the dyad axis can be
set:
- odd symmetric - The axis is on a single base,
so that the site contains an odd number of bases.
Examples:
gallery of 8 logos:
lambda cI and cro and Lambda O.
- even symmetric - The axis is between two bases,
so that the site contains an even number of bases.
Examples:
gallery of 8 logos:
434 cI and cro,
ArgR,
CRP,
TrpR,
FNR,
LexA.
Placement of zero coordinate:
For consistency,
one can place the
zero coordinate
on a binding site according to its symmetry
and some simple rules.
- Asymmetric sites:
at a position of high sequence conservation
or the start of transcription or translation
- Odd symmetry site: at the center of the site
- Even symmetry site:
for simplicity,
the suggested convention is to place the
zero base
on the 5' side of the axis so that the bases 0 and 1 surround the axis.
Within the
Delila
system, the
instshift
program makes readjusting the zero coordinate easy.
The Symmetry Paradox:
Note that specific individual sites may not be symmetrical
(i.e. completely self-complementary)
even though
the set of all sites are bound symmetrically.
This raises an odd experimental problem. How do we know that
a site is symmetric when bound by a dimeric protein if each individual
site has variation on the two sides?
If we assume that the site is symmetrical,
then we would write
Delila instructions
for both the sequence and its complement.
The resulting
sequence logo
will, by definition be symmetrical.
If, on the other hand, we write the instructions so as to take only
one orientation from each sequence, perhaps arbitrarily,
then
by definition the logo will be asymmetrical.
That is, one gets the output of what one puts in.
This is a serious philosophical and practical problem for creating
good models of binding sites.
One solution would be to use a model that has the maximum
information
content
although this may be difficult to determine in many cases because of
small sample sizes.
Another solution is to orient the sites by some biological
criterion, such as the direction of transcription controlled
by an activator.
See also:
bit:
A binary digit, or
the amount of
information
required to distinguish between two equally likely possibilities or
choices.
If I tell you that a coin
is 'heads' then you learn one bit of information.
It's like a knife slice between the possibilities:
Likewise, if a protein picks one of the 4 bases,
then it makes a two bit choice.
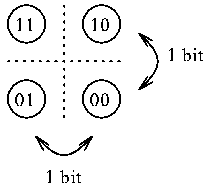
For 8 things it takes 3
bits.
In simple cases the number of bits is the log base 2
of the number of choices or
messages
M:
bits = log2M.
Claude Shannon
figured out how to compute the average information
when the choices are not equally likely.
The reason for using this measure
is that when
two communication systems are independent,
the number of bits is additive.
The log is the only mathematical measure that has this property!
Both of the properties of averaging and additivity
are important for
sequence logos
and
sequence walkers.
Even in the early days of computers and information theory
people recognized that there were already two definitions
of bit and that nothing could be done about it.
The most common definition is 'binary digit',
usually a 0 or a 1 in a computer.
This definition allows only for two integer values.
The definition that Shannon came up with is an
average number of bits that describes an
entire communication
message
(or, in molecular biology,
a set of aligned protein sequences
or nucleic-acid
binding sites).
This latter definition allows for real numbers.
Fortunately the two definitions can be distinguished
by context.
See also:
BITCS:
Biological Information Theory and Chowder Society.
An eclectic group of folks from around the planet
who are interested in the application
of information theory in biology.
Discussions are held on
bionet.info-theory
and there is a
FAQ available.
blind alley:
Avoiding blind alleys is hard. How do you know a path is blind
without going into it? If you are a true explorer, you cannot trust
another explorer's word that a certain way is blocked
- maybe there is a way through that you will
see. The most important thing is to go into interesting paths and
explore them. It is important to be able to identify a path as a dead
end (for you) and then to WALK OUT again. People usually just hang
around and get stuck with lots of bad ideas in their heads. One
example is to think that one's model is reality.
See:
pitfall
and
pitfalls in molecular information theory.
Boltzmann:
Ludwig Boltzmann
was a famous thermodynamicist who recognized that
entropy
is a measure of the number of ways
(W)
that energy can be configured
in a system:
S = K log W
This formula is on
Boltzmann's Tomb in the Zentralfriedhof (Central Cemetary).
Vienna, Austria. See also:
book:
A collection of DNA sequences in the
Delila system.
Books are usually created by
the
delila
program, but can also be created by
dbbk,
rawbk,
and
makebk.
The unique feature of Delila books is that they carry a
coordinate system that defines the coordinates of each
base in the book. This makes the Delila program powerful
because one can use Delila to extract parts of sequences and
maintain the original coordinates.
See also library.
box:
Poor Terminology!
A region of sequence with a particular function.
A
sequence logo
of a
binding site
will often reveal that there is significant
sequence conservation
`outside' the box. The term `core' is sometimes
used to acknowledge this, but sequence logos reveal that
the division is an arbitrary convention and therefore not
biologically meaningful.
Recommendation:
replace this concept with
binding site for nucleic acids
or
`motif'
for proteins.
Example:
In the paper
"Ordered and sequential binding of DnaA protein to
oriC, the chromosomal origin of Escherichia coli".
Margulies C, Kaguni JM.
J Biol Chem 1996 Jul 19;271(29):17035-40,
the authors use the conventional model that DnaA binds to 9 bases
and they call the sites "boxes".
However, in the paper they demonstrate that there are effects
of the sequence outside the "box", which demonstrates
that the "box" is an artifact.
byte: A binary string consisting of 8
bits.
certainty:
'Certainty' is not defined in information theory. However,
Claude Shannon
apparently discovered that one can measure
uncertainty.
By implication, there is no measure for 'certainty'. The best one can
have is a decrease of uncertainty, and this is Shannon's
information
measure.
The uncertainty before an event (e.g. receiving a
symbol) less
the equivocation (uncertainty after the event) is the information.
Since there is always
thermal noise,
there is always equivocation, so
there is never absolute certainty.
See:
uncertainty.
channel capacity, channel capacity theorem:
The maximum information, in bits per second, that a communications
channel can handle is:
See also:
book:
A collection of DNA sequences in the
Delila system.
Books are usually created by
the
delila
program, but can also be created by
dbbk,
rawbk,
and
makebk.
The unique feature of Delila books is that they carry a
coordinate system that defines the coordinates of each
base in the book. This makes the Delila program powerful
because one can use Delila to extract parts of sequences and
maintain the original coordinates.
See also library.
box:
Poor Terminology!
A region of sequence with a particular function.
A
sequence logo
of a
binding site
will often reveal that there is significant
sequence conservation
`outside' the box. The term `core' is sometimes
used to acknowledge this, but sequence logos reveal that
the division is an arbitrary convention and therefore not
biologically meaningful.
Recommendation:
replace this concept with
binding site for nucleic acids
or
`motif'
for proteins.
Example:
In the paper
"Ordered and sequential binding of DnaA protein to
oriC, the chromosomal origin of Escherichia coli".
Margulies C, Kaguni JM.
J Biol Chem 1996 Jul 19;271(29):17035-40,
the authors use the conventional model that DnaA binds to 9 bases
and they call the sites "boxes".
However, in the paper they demonstrate that there are effects
of the sequence outside the "box", which demonstrates
that the "box" is an artifact.
byte: A binary string consisting of 8
bits.
certainty:
'Certainty' is not defined in information theory. However,
Claude Shannon
apparently discovered that one can measure
uncertainty.
By implication, there is no measure for 'certainty'. The best one can
have is a decrease of uncertainty, and this is Shannon's
information
measure.
The uncertainty before an event (e.g. receiving a
symbol) less
the equivocation (uncertainty after the event) is the information.
Since there is always
thermal noise,
there is always equivocation, so
there is never absolute certainty.
See:
uncertainty.
channel capacity, channel capacity theorem:
The maximum information, in bits per second, that a communications
channel can handle is:
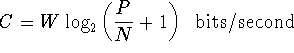
where
W is the bandwidth (cycles per second = hertz),
P is the received power (joules per second)
and
N is the
noise
(joules per second).
Shannon
derived this formula by realizing that
each received
message
can be represented as a sphere in a high dimensional space.
The maximum number of messages is determined by
the diameter of these spheres
and the available space.
The diameter of the spheres is determined by the
noise
and the available space is a sphere determined by the total power
and the noise.
Shannon realized that by dividing the volume of the larger
sphere by the volume of the smaller message spheres,
one would obtain the maximum number of messages.
The logarithm (base 2) of this number is the channel capacity.
In the formula, the
signal-to-noise ratio
is P/N.
Shannon's channel capacity theorem states that if one attempts
to transmit information at a rate R greater than C only
at best C bits per second will be received.
On the other hand
if R is less than or equal to C
then
one may have as few errors as desired,
so long as the channel is properly coded.
As a consequence of this theorem, many methods of coding
have been derived, and as a result we now have
satellite communications,
the internet,
CDs, DVD's and wireless communications.
A similar formula applies to biology.
See also:
choice:
The process whereby a living being (or part of one)
discriminates between two or more symbols. For example, the EcoRI
restriction enzyme binds to the pattern 5' GAATTC 3' in DNA.
It avoids all other 6
long sequences. If you mix the enzyme with DNA, the DNA is cut between
the G and A. That is, it is a molecule that picks GAATTC from all
other patterns. It makes choices. Furthermore you can measure the
number of choices in bits: 12 bits.
See also:
code (coding, coding theory):
Coding is the representation of a
message
into a form
suitable for transmission over a communications line.
This protects the message from noise.
Since messages can be represented by points in a high dimensional space
(the first bit is the first dimension, the second bit is the second
dimension, etc.,
see
message),
the coding corresponds to the placement of the messages relative
to each other in the high dimensional space.
This concept is from
Shannon's 1949 paper.
When a message has been received,
it has been distorted by
thermal noise, and in the high dimensional space
the noise distorts the initial transmitted
message point in all directions evenly.
The final result is that each received
message is represented by a point somewhere on a sphere.
Decoding the message corresponds to finding the nearest sphere center.
Picking a code corresponds to figuring out how the spheres should
be placed relative to each other so that they are distinguishable by
not overlapping.
This situation can be represented by a
gumball machine.
Shannon's
famous work on information theory
was frustrating in the sense that he proved that codes exist
that can reduce
error rates
to as low as one may desire (since
at high dimensions the
spheres become sharp edged),
but he did not say how this could be accomplished.
Fortunately a large effort by many people
established many kinds of communications codes,
and of course the development of electronic chips
allows decoding in a small device.
The result is
that we now have many means of clear communications, such as
CDs, MP3, DVD, the internet, and digital wireless cell phones.
One of the most famous coding theorists was
Hamming.
An example of a simple code that protects a message against
error is the
parity_bit.
Codes exist in
biology
and
molecular biology
not only in the genetic code but
also there must be a code for every specific interaction
made by
molecular machines.
In many of these cases the spheres represent states of molecules
instead of messages.
See also:
communication:
for information theory,
communication is a process in which
the state at a
transmitter,
a source of
information,
is reproduced with some
errors
at a receiver.
The errors are caused by
noise
in the communications channel.
complexity:
Poor Terminology!
Like
`specificity',
the term `complexity' appears in many scientific papers,
but it is not always well defined.
(See however
M. Li and P. Vitanyi,
A Introduction to Kolmogorov Complexity and Its Applications,
second edition,
Springer-Verlag,
New York,
ISBN 0-387-94868-6,
1997)
When one comes across a proposed use
in the literature one can unveil this difficulty by asking:
How would I measure this complexity?
What are the units of complexity?
Recommendation:
use Shannon's
information measure
or
explain why Shannon's measure does not cover what you
are interested in measuring.
Then give a precise, practical definition.
consensus sequence (consensus):
Poor Terminology!
The simplest form of a consensus sequence
is created by picking
the most frequent base
at some position in a set of
aligned
DNA, RNA or protein
sequences such as
binding sites.
The process of creating a consensus destroys the
frequency information and leads to many errors in interpreting
sequences.
It is one of the worst
pitfalls
in molecular biology.
Suppose a position in a binding site had 75% A. The consensus
would be A. Later, after having forgotten
the origin of the consensus while trying to make a prediction,
one would be wrong 25% of the
time. If this is done over all the positions of a binding site,
most predicted sites can be wrong!
For example,
in
Rogan
and Schneider (1995)
a case is shown where a patient was misdiagnosed
because a consensus sequence was used to interpret
a sequence change in a splice junction.
Figure 2
of the
sequence walker paper shows a Fis binding site that had been
missed because it did not fit a consensus model.
Recommendation:
one can entirely replace this concept with
sequence logos
and
sequence walkers.
See also
coordinate system of sequences:
A coordinate system is
the numbering system of a nucleic acid or protein sequence.
Coordinate
systems in primary databases such as GenBank and PIR are usually
1-to-n,
where n is the length of the sequence,
so they are not recorded in the database. However, in the
Delila system, one can extract sequence
fragments from a larger database. If one does two extractions,
then one can go slightly crazy trying to match up sequence coordinates
if the numbering of the new sequence is still
1-to-n.
The Delila system handles all continuous coordinate systems, both
linear and circular, as described in
LIBDEF,
the definition of the DELILA database system.
For example, on a circular sequence running from 1 to 100, the
Delila instruction
get from 10 to 90 direction -;
will give a coordinate system that runs from 10 down
to 1, and then continues from 100 down to 90.
- Unfortunately there are many examples in the literature of nucleic-acid
coordinate systems
without a
zero coordinate.
A zero base is useful when one is identifying the locations
of sequence walkers: the location of the predicted binding site
is the zero base of the walker (the vertical rectangle).
Without a zero base,
it would be tricky to determine the
positions of bases in a sequence walker.
With a zero base it is quite natural.
- Insertion or deletions will make holes or extra parts
of a coordinate system.
The Delila system cannot handle these (yet). In the meantime, the sequences
are renumbered to create a continuous coordinate system.
- See:
PhilGen: Philosophy and Definition for a Universal Genetic
Sequence Database .
core consensus:
Poor Terminology!
A core consensus is
the strongly conserved portion of a
binding site
found by creating a
consensus sequence.
It is an
arbitrary definition as can be seen from the examples in the
sequence logo gallery.
The sequence conservation,
measured in
bits
of
information,
often follows the cosine waves that
represent the twist of B-form DNA.
This has been explained
by noting that a protein bouncing in and out from DNA must
evolve contacts.
It is easier to evolve DNA contacts that are close to the
protein than those that are further around the helix. Because the sequence
conservation varies continuously,
any cutoff or "core" is
arbitrary.
Recommendation:
replace this concept with
sequence logos
and
sequence walkers.
See also:
- oxyr paper:
T. D. Schneider.
Reading of DNA sequence logos: Prediction of major groove binding
by information theory.
Meth. Enzym., 274:445-455, 1996.
- baseflip paper:
T. D. Schneider.
Strong minor groove base conservation in sequence logos implies DNA
distortion or base flipping during replication and transcription initiation.
Nucl. Acid Res., 29(23):4881-4891, 2001.
Delila:
stands for
DEoxyribonucleic-acid
LIbrary
LAnguage.
It is a language for extracting DNA fragments from a large collection of
sequences, invented around 1980
(T. D. Schneider,
G. D. Stormo,
J. S. Haemer,
and L. Gold",
A design for computer nucleic-acid sequence storage, retrieval and
manipulation,
Nucl. Acids Res.,
10:
3013-3024,
1982).
The idea is that there is a large database containing all the sequences
one would like, which we call a `library'.
(It is amusing and appropriate that
GenBank
now resides at the
National Library of Medicine
in the
National Center for Biotechnology Information!)
One would like a particular subset of these sequences, so one writes
up some instructions and gives them to the librarian, Delila,
which returns a
`book'
containing just the sequences
one wants for a particular analysis.
So `Delila' also stands for the program that does the extraction
(delila.p).
Since it is easier to manipulate Delila instructions than to
edit DNA sequences, one makes fewer mistakes
in generating one's data set for analysis,
and they are trivial to correct.
Also, a number of programs create instructions, which provides
a powerful means of sequence manipulation.
One of Delila's strengths is that it can handle any continuous
coordinate system.
The `Delila system' refers to
a set of programs
that use these sequence subsets for
molecular information theory
analysis of
binding sites
and proteins.
In the spring of 1999 Delila became capable of making sequence mutations,
which can be displayed graphically along with
sequence walkers
on a lister map.
A complete definition
for the language is available
(LIBDEF),
although not all of it is implemented.
There are also tutorials on
building Delila libraries
and
using Delila instructions.
A web-based
Delila server
is available.
Delila instructions:
a set of detailed instructions for obtaining specific nucleic-acid
sequences from a sequence database.
The instructions are written in
a computer language called
Delila.
There is a
short
tutorial on using Delila instructions.
digit:
The set of symbols 0 to 9,
specifying the choice of one thing in 10.
Therefore, like the
bit,
a digit is a measure of an amount of
information.
While bits are determined by using log base 2, digits are determined
by taking log base 10 (and adding 1). So the number 1000 is
log101000 + 1 = 3 + 1 = 4 digits.
It's not clear to my why one adds 1, but certainly the number of digits
in a number follows this formula.
However in the case of 1, we would like to say that there is one digit,
so log101 + 1 = 0 + 1 = 1 digit.
donor splice site:
The binding site of the spliceosome
on the 5' side of an intron and the 3' side of an exon.
This term is preferred over "5' site" because there can
be multiple donor sites, in which case "5' site" is
ambiguous.
Also, one would have to refer to the 5' site on the 3' side
of an exon, which is confusing.
Mechanistically, a donor site defines the end of the exon,
not the other way around.
See
 efficiency:
the amount of energy applied to a useful purpose in a system
compared to the total energy dissipated.
The Carnot efficiency functions between two temperatures.
This is not appropriate for most biological systems since biological
systems generally function at one temperature.
An efficiency defined by Pierce and Cuttler in 1959 applies
to isothermal systems. It is computed by dividing the
information
gained by the energy dissipated, when the energy has been
converted to bits using
the
Second Law of Thermodynamics
in the form
Emin = kB T ln(2) = -q/R (joules per bit).
See
entropy: A measure of the state of a system that can roughly
be interpreted as the randomness of the energy in a system.
Since the entropy concept in thermodynamics and chemistry
has units of energy per temperature (Joules/Kelvin),
while the
uncertainty measure
from Claude Shannon
has
units of bits per symbol,
it is best to keep these concepts distinct.
The Boltzmann form for entropy is:
while the Shannon form for uncertainty is:
See also:
error:
In communications, the substitution of one symbol
for another in a
received
message
caused by
noise.
Shannon's
channel capacity theorem showed that
it is possible to build systems with as low an error as desired,
but one cannot avoid errors entirely.
Evolution of Biological Information:
The information of
patterns
in nucleic acid
binding sites
can be measured as
Rsequence
(the area under a
sequence logo).
The amount of information
needed to find the binding sites,
Rfrequency,
can be predicted from the size
of the genome and number of binding sites.
Rfrequency is fixed by the current physiology of an organism but
Rsequence can vary.
A computer simulation shows that
the information in the binding sites (Rsequence)
does indeed evolve toward the information needed to locate
the binding sites (Rfrequency).
See:
flip-flop:
A flip-flop is a two-state device. A common example is a light
switch. Flip-flops can store one
bit
of
information.
See also
frequency:
A measured
number of occurances of an event
in a sample population.
See also:
from: The 5' extent of the range of a binding site.
For example in a
Delila instruction
one might have
get from 50 -10 to
same +5; the range runs from -10 to +5.
genetic control system:
a set of one or more genes controlled by proteins or RNAs.
There are thousands of examples.
The most famous is the Lac repressor system,
which was the first one understood.
Jacob and Monod used elegant genetics
to figure out how it worked.
Basically a protein called the Lac Repressor binds to the
DNA and so blocks transcription.
Another famous system is the bacteriophage lambda cI repressor
and cro system.
There is a vast and rapidly growing literature
as people figure out control systems in all the different organisms.
Genetic control systems are involved in developmental biology,
so the structure of animals and plants is determined by them.
Many diseases are result of ruined or partially ruined controls.
For example, 15% of all single point mutations that cause genetic
diseases in humans are in splice junctions
(donor
and
acceptor
splice sites)
(
Krawczak M, Reiss J, Cooper DN.,
Hum Genet. 1992 Sep-Oct;90(1-2):41-54.),
which are
part of a genetic control system that splices mRNA.
Much of the rest of
this web site
has
sequence logos
for many genetic
systems that we have analyzed. You can explore that too.
See also:
genome:
The complete genetic material of an organism.
It can be either DNA or RNA.
For example,
the genome of the bacterium E. coli
is about 4.7 million base pairs of DNA
and has about 4,000 genes.
By contrast
a human has about
3 billion base pairs of DNA
and has
20,000 to 25,000 genes.
You can find the complete genomes of many organisms
at
GenBank.
When computing the information needed to locate
a set of
binding sites in a genome,
the number of positions that a protein or other molecule
can bind is counted.
This may not be the number of base pairs.
See the discussion of
Rfrequency for further explanation.
genomic skew:
The frequencies of bases in the genome of an organism
are not always equiprobable.
For example,
the composition can have high "GC" content relative to the "AT".
If one makes a sequence logo, this can appear as a background
information outside the binding sites.
Many people immediately assume that it should be removed.
This can generally be done by computing the genomic
uncertainty and using that for
Hbefore.
However, this implies an interpretation of the phenomenon, and
the cause of 'skew' is not understood.
Some possibilities include strong biases in mutation or DNA repair.
Alternatively, histone-like proteins could be binding
all over the genome, in which case it would be inappropriate
to remove the pattern, as it represents the actual information
of a binding protein!
For further discussion, see also:
efficiency:
the amount of energy applied to a useful purpose in a system
compared to the total energy dissipated.
The Carnot efficiency functions between two temperatures.
This is not appropriate for most biological systems since biological
systems generally function at one temperature.
An efficiency defined by Pierce and Cuttler in 1959 applies
to isothermal systems. It is computed by dividing the
information
gained by the energy dissipated, when the energy has been
converted to bits using
the
Second Law of Thermodynamics
in the form
Emin = kB T ln(2) = -q/R (joules per bit).
See
entropy: A measure of the state of a system that can roughly
be interpreted as the randomness of the energy in a system.
Since the entropy concept in thermodynamics and chemistry
has units of energy per temperature (Joules/Kelvin),
while the
uncertainty measure
from Claude Shannon
has
units of bits per symbol,
it is best to keep these concepts distinct.
The Boltzmann form for entropy is:
while the Shannon form for uncertainty is:
See also:
error:
In communications, the substitution of one symbol
for another in a
received
message
caused by
noise.
Shannon's
channel capacity theorem showed that
it is possible to build systems with as low an error as desired,
but one cannot avoid errors entirely.
Evolution of Biological Information:
The information of
patterns
in nucleic acid
binding sites
can be measured as
Rsequence
(the area under a
sequence logo).
The amount of information
needed to find the binding sites,
Rfrequency,
can be predicted from the size
of the genome and number of binding sites.
Rfrequency is fixed by the current physiology of an organism but
Rsequence can vary.
A computer simulation shows that
the information in the binding sites (Rsequence)
does indeed evolve toward the information needed to locate
the binding sites (Rfrequency).
See:
flip-flop:
A flip-flop is a two-state device. A common example is a light
switch. Flip-flops can store one
bit
of
information.
See also
frequency:
A measured
number of occurances of an event
in a sample population.
See also:
from: The 5' extent of the range of a binding site.
For example in a
Delila instruction
one might have
get from 50 -10 to
same +5; the range runs from -10 to +5.
genetic control system:
a set of one or more genes controlled by proteins or RNAs.
There are thousands of examples.
The most famous is the Lac repressor system,
which was the first one understood.
Jacob and Monod used elegant genetics
to figure out how it worked.
Basically a protein called the Lac Repressor binds to the
DNA and so blocks transcription.
Another famous system is the bacteriophage lambda cI repressor
and cro system.
There is a vast and rapidly growing literature
as people figure out control systems in all the different organisms.
Genetic control systems are involved in developmental biology,
so the structure of animals and plants is determined by them.
Many diseases are result of ruined or partially ruined controls.
For example, 15% of all single point mutations that cause genetic
diseases in humans are in splice junctions
(donor
and
acceptor
splice sites)
(
Krawczak M, Reiss J, Cooper DN.,
Hum Genet. 1992 Sep-Oct;90(1-2):41-54.),
which are
part of a genetic control system that splices mRNA.
Much of the rest of
this web site
has
sequence logos
for many genetic
systems that we have analyzed. You can explore that too.
See also:
genome:
The complete genetic material of an organism.
It can be either DNA or RNA.
For example,
the genome of the bacterium E. coli
is about 4.7 million base pairs of DNA
and has about 4,000 genes.
By contrast
a human has about
3 billion base pairs of DNA
and has
20,000 to 25,000 genes.
You can find the complete genomes of many organisms
at
GenBank.
When computing the information needed to locate
a set of
binding sites in a genome,
the number of positions that a protein or other molecule
can bind is counted.
This may not be the number of base pairs.
See the discussion of
Rfrequency for further explanation.
genomic skew:
The frequencies of bases in the genome of an organism
are not always equiprobable.
For example,
the composition can have high "GC" content relative to the "AT".
If one makes a sequence logo, this can appear as a background
information outside the binding sites.
Many people immediately assume that it should be removed.
This can generally be done by computing the genomic
uncertainty and using that for
Hbefore.
However, this implies an interpretation of the phenomenon, and
the cause of 'skew' is not understood.
Some possibilities include strong biases in mutation or DNA repair.
Alternatively, histone-like proteins could be binding
all over the genome, in which case it would be inappropriate
to remove the pattern, as it represents the actual information
of a binding protein!
For further discussion, see also:
- Information Content of Binding Sites,
the original discussion on this topic.
I never agreed with the R* formula given in this paper,
but only put it in under duress and out of fairness
for an alternative view point.
NOTE that the R* formula can give values greater than 2 for
a base. This means that R* is not part of information theory
and it is not a measure in bits because
it never takes more than 2 bits to chose one base in 4.
- Measuring Molecular Information, equation 6 and the text following.
- Evolution of Biological Information, Discussion.
 gumball machine:
A model for the packing of
Shannon
spheres. Each gumball represents
one possible message or one possible molecular state
(an after sphere).
The radius of the gumball represents the
thermal noise.
The balls are all enclosed inside a larger sphere
(the before sphere)
whose radius
is determined from both the thermal noise and the power dissipated
at the receiver (or by the molecule) while it selects that state.
The way the spheres are packed relative to each other is the
coding.
See channel capacity
and molecular machine capacity.
Richard W. Hamming: An engineer at Bell Labs in the 1940s who
wrote the famous book
"Coding and Information Theory"
which explains
coding theory.
See also:
hypersphere:
See Shannon sphere.
Independence:
two variables are independent when
a change of one of them does not alter the value of the other.
We often assume that positions across a
binding site
are independent.
This is a major assumption for
sequence logos.
The idea that different parts of a binding site are independent is a
useful initial assumption.
However,
there is some literature on the subject of non-independence
and Gary Stormo has written on it.
In cases when there is enough data,
one can test the assumption -
in our 1992 paper on splicing we did and found no correlations for the
acceptors and a small amount for donors.
The likely reason for the general observation of independence
in binding sites is pretty simple.
The DNA or RNA lies in a groove on the surface of the molecule.
Aside from neighboring bases, a complex system of correlations
would be hard to evolve because it would require mechanisms running
through the
recognizer.
So they evolve, for the most part, not to have correlations.
gumball machine:
A model for the packing of
Shannon
spheres. Each gumball represents
one possible message or one possible molecular state
(an after sphere).
The radius of the gumball represents the
thermal noise.
The balls are all enclosed inside a larger sphere
(the before sphere)
whose radius
is determined from both the thermal noise and the power dissipated
at the receiver (or by the molecule) while it selects that state.
The way the spheres are packed relative to each other is the
coding.
See channel capacity
and molecular machine capacity.
Richard W. Hamming: An engineer at Bell Labs in the 1940s who
wrote the famous book
"Coding and Information Theory"
which explains
coding theory.
See also:
hypersphere:
See Shannon sphere.
Independence:
two variables are independent when
a change of one of them does not alter the value of the other.
We often assume that positions across a
binding site
are independent.
This is a major assumption for
sequence logos.
The idea that different parts of a binding site are independent is a
useful initial assumption.
However,
there is some literature on the subject of non-independence
and Gary Stormo has written on it.
In cases when there is enough data,
one can test the assumption -
in our 1992 paper on splicing we did and found no correlations for the
acceptors and a small amount for donors.
The likely reason for the general observation of independence
in binding sites is pretty simple.
The DNA or RNA lies in a groove on the surface of the molecule.
Aside from neighboring bases, a complex system of correlations
would be hard to evolve because it would require mechanisms running
through the
recognizer.
So they evolve, for the most part, not to have correlations.
Independence plays a vital role in information theory.
When two communications channels
are independent, the information of each can be added.
Because he wanted an additive measure,
Shannon demanded this and found (as others before him) that
the log function has the necessary property.
For example,
suppose we have two channels, one has two symbols H and T (for heads
and tails) and the other has four symbols a, c, g, t (for the four
bases). Then the first can carry 1 bit (log22 = 1)
and the second can carry 2 bits (log24 = 2).
A combined channel has eight symbols
(Ha, Hc, Hg, Ht,
Ta, Tc, Tg, Tt) and
can carry 3 bits (log28 = 3).
That is, you can multiply the possibilities or you can add the logs.
Independence plays an elegant role in Shannon's
construction of the channel capacity in his
1949 paper.
In this case it is worth noting that if two variables are
independent, this can be represented geometrically as two
orthogonal axes
(at 90 degrees to each other).
See also:
-
Features of spliceosome evolution and function
inferred from an analysis of the information at human splice sites".
R. M. Stephens and T. D. Schneider,
J. Mol. Biol.,
228,
1124-1136.
See section 3b:
Materials and Methods, statistical tests,
which describes how to compute the correlation between
two positions in a binding site in bits.
-
Non-independence of Mnt repressor-operator interaction determined by
a new quantitative multiple fluorescence relative affinity (QuMFRA)
assay.
Nucleic Acids Res. 2001 Jun 15;29(12):2471-8.
Man TK, Stormo GD.
-
Additivity in protein-DNA interactions: how good an approximation is it?
Nucleic Acids Res. 2002 Oct 15;30(20):4442-51.
Benos PV, Bulyk ML, Stormo GD.
"We conclude that despite the fact that the additivity assumption does
not fit the data perfectly, in most cases it provides a very good
approximation of the true nature of the specific protein-DNA
interactions. Therefore, additive models can be very useful for the
discovery and prediction of binding sites in genomic DNA."
-
Shannon 1949.
individual information: the
information
that a single
binding site
contributes to the sequence conservation of a set of binding sites.
This can be graphically displayed by a
sequence walker.
It is computed as the decrease in
surprisal
between the
before state
and the
after state.
The technical name is Ri.
See also:
ridebate.
information: Information is measured as the decrease in
uncertainty
of a receiver or
molecular machine
in going from the
before state
to the
after state.
"In spite of this dependence on the coordinate system the entropy concept
is as important in the continuous case as the discrete case. This is
due to the fact that the derived concepts of information rate and
channel capacity depend on the difference of two entropies
and this difference does not depend on the coordinate frame, each
of the two terms being changed by the same amount."
--- Claude Shannon,
A Mathematical Theory of Communication,
Part III, section 20, number 3
Information is usually measured in
bits per second
or bits per
molecular machine operation.
See also:
-
Information Is Not Entropy, Information Is Not Uncertainty!.
-
information theory.
- Evolution of biological information
- Reviews of the book:
A Mind at Play by Jimmy Soni and Rob Goodman, 2017
-
A Man in a Hurry: Claude Shannon's New York Years. By day,
Claude Shannon labored on top-secret war projects at Bell Labs.
By night, he worked out the details of information theory.,
by Jimmy Soni and Rob Goodman, 12 Jul 2017.
-
How Information Got Re-Invented.
The story behind the birth of the information age,
by Jimmy Soni and Rob Goodman, August 10, 2017.
-
The bit bomb. It took a polymath to pin down the true nature of
`information'. His answer was both a revelation and a return,
by Rob Goodman and Jimmy Soni, 30 August, 2017.
information theory:
Information theory is
a branch of mathematics founded by
Claude Shannon
in the 1940s.
The theory addresses two aspects of communication:
"How can we define and measure
information?"
and
"What is the maximum information that can be sent through
a communications channel?"
(channel capacity).
See also:
 isothermal efficiency:
A measure of how a system uses energy when functioning at only
one temperature.
isothermal efficiency:
A measure of how a system uses energy when functioning at only
one temperature.
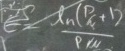 See
junk_DNA:
regions of a genome for which we do not know a function.
Calling large parts of the genome
'junk' is possibly the height of human egotism,
unless it stands for J.U.N.K:
Just Use Not Known.
leaky mutation:
a weak
mutation.
For example,
figure 2 in Rogan.Faux.Schneider1998.
library:
A DNA sequence database in the
Delila system.
A library is created by running the
catal
program,
which ensures that
sequence fragments in the library do have the duplicated names.
See also book.
lister feature:
A graphical object marking a sequence on a
lister map.
Features are defined once and then may be used many times.
Features can be either ASCII (i.e. text) strings or
sequence walkers.
In either case the
lister
program arranges the locations of the features so that they
do not overlap.
Programs that generate features are
scan
and
search.
See also:
lister mark,
lister map.
lister map: A graphical display of
one or more sequences marked with
protein translations,
colored marks (generally arrows and boxes
but also
cyclic waves),
ASCII features (such as footprinted regions,
exons
and
RNA structures)
and
sequence walkers.
The map is produced by the
lister
program. Some examples:
See
junk_DNA:
regions of a genome for which we do not know a function.
Calling large parts of the genome
'junk' is possibly the height of human egotism,
unless it stands for J.U.N.K:
Just Use Not Known.
leaky mutation:
a weak
mutation.
For example,
figure 2 in Rogan.Faux.Schneider1998.
library:
A DNA sequence database in the
Delila system.
A library is created by running the
catal
program,
which ensures that
sequence fragments in the library do have the duplicated names.
See also book.
lister feature:
A graphical object marking a sequence on a
lister map.
Features are defined once and then may be used many times.
Features can be either ASCII (i.e. text) strings or
sequence walkers.
In either case the
lister
program arranges the locations of the features so that they
do not overlap.
Programs that generate features are
scan
and
search.
See also:
lister mark,
lister map.
lister map: A graphical display of
one or more sequences marked with
protein translations,
colored marks (generally arrows and boxes
but also
cyclic waves),
ASCII features (such as footprinted regions,
exons
and
RNA structures)
and
sequence walkers.
The map is produced by the
lister
program. Some examples:
- One of Tom's
favorite examples
shows a lister map for a
mutation
that causes vision loss.
- An example of marks and features
on a lister map is
Zheng et. al
J Bacteriol 1999 Aug;181(15):4639-43, Figure 1.
A walker for OxyR was discovered in front of the Fur promoter.
Footprinting subsequently showed that the protected region
exactly covers the sequence walker.
- Another beautiful example is the
Fis promoter
which has many Fis sites of various strengths overlapping promoters.
- Below is a lister map of the famous LacZ promoter region.
It contains:
- DNA sequence numbered every 10 bases with tic marks ('*') every 5
so you never go crazy counting bases
- sites:
- Each kind of site has a different colored rectangle behind it,
called a "petal" (as in the petals of a flower). The coloring
is determined using hue, saturation and brightness. The brightness
is set to 1 (fully bright). The hue is associated with the kind
of binding site (blue, yellow, red, purple, cyan and green in this case).
The saturation of a site indicates how strong it is. This is
computed by dividing the site strength in bits by the
bits for the strongest possible site (the "consensus",
see Consensus Sequence Zen).
- Sites that are symmetrical have letters up and down (Crp and LacI)
while sites that are asymmetrical have sideways letters.
The direction you would read these 'downward' is the direction the
site points (sigma 70 and ribosome binding sites).
- Sites have a sine wave on them to indicate the orientation
on the DNA. See:
baseflip.
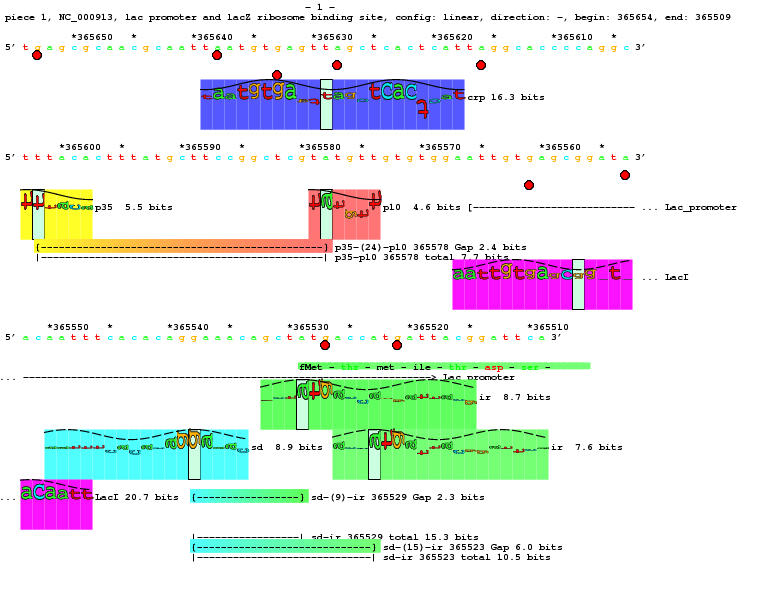
See also:
lister mark or mark:
A graphical object associated
with a sequence on a
lister map
or
sequence logo.
Marks are defined entirely by coordinate position and
do not displace features or other marks.
They are placed at the time that the coordinate is encountered by
lister
and follow the
postscript
rule that younger marks are written on top of older ones.
This allows one to place
boxes around sequence walkers, for example, by placing the mark
for a box before the walker coordinate.
Marks must be given strictly in the order of the
book sequences.
When sequence polymorphisms or mutations are generated
by the
delila program,
they are recorded using the marksdelila file.
The
live
program generates cyclic marks along the sequence
and can be used to indicate
the face of the DNA or the reading frame.
A user can also define their own kind of marks using
PostScript.
A set of marks can be merged with other marks
using the
mergemarks program.
See also:
lister feature,
lister map,
makelogo,
marks.arrow,
libdef examples of marksdelila.
logo:
See:
sequence logo.
map: See lister map.
Maxwell's demon: A mythical beast invented by James Maxwell in 1867.
The demon supposedly violates the
Second Law of Thermodynamics.
However, a careful analysis from the perspective of molecular biology
indicates that such a creature is not possible to construct
given our current knowledge of atoms, myosin, actin and rhodopsin
(see nano2).
meaning:
In his 1948 paper,
Shannon explicitly set aside value and meaning in his exposition
of
information theory:
Frequently the messages have meaning; that is they refer to or are
correlated according to some system with certain physical or
conceptual entities. These semantic aspects of communication are
irrelevant to the engineering problem.
But what is meaning? Many have struggled with this question.
I (TDS) thought of meaning as the interpretation of
information by a being, but a clear exposition is given by
Anthony Reading in
Information 2012, 3, 635-643 When Information Conveys Meaning.
His definition:
Meaningful information is thus conceptualized here as patterns of
matter and energy that have a tangible effect on the entities that
detect them, either by changing their function, structure or behavior,
while patterns of matter and energy that have no such effects are
considered meaningless.
message:
A message is
a series of symbols chosen from a predefined alphabet.
In molecular biology the term `message' usually refers to a messenger RNA.
In
molecular information theory,
a message corresponds to an
after state
of a
molecular machine.
In
information theory,
Shannon
proposed to represent a message as a
point in a high dimensional space
(see
Shannon1949).
For example, if we send three independent voltage pulses, their heights
correspond to a point in three-dimensional space.
A message consisting
of 100 pulses corresponds to a point in 100 dimensional space.
Starting from this concept, Shannon derived the
channel capacity.
See also:
mismatches:
Poor Terminology!
The number of mismatches is
a count of the number of differences
between a given sequence
and a
consensus sequence.
For example,
a friend wrote
"This
binding site
has three mismatches in non-critical positions."
If one wants to note that a position
in a binding site
has negative information
in a
sequence walker,
then one can say that it has negative information!
A base in a site could have a mismatch
to the consensus
and yet
that base could contribute positive information.
For example for a position that has
60% A,
30% T,
5% G,
and
5% C
the consensus base is A by two-fold, and yet
a T in an individual binding site
would contribute 2 + log20.30 = 0.26 bits.
Chari (Krishnamachari Annangarachari) pointed out that
the lesson is to
"see things in totality, not in isolation".
That is, only by noting the total distribution can
we learn that the T contributes positively to the total
information.
He also pointed out that this is a lesson in
"unity in diversity".
The logo shows
both the unity of the binding site and simultaneously
shows its diversity.
See also:
molecular biology:
The study of biology at the molecular level.
Molecular biologists have no fear of stealing from adjacent
scientific fields.
When they discovered the structure of DNA
Watson and Crick
used ideas from physics,
genetics and biochemistry (already a conglomeration
of biology and chemistry).
This web site is all about stealing
information theory and taming it for molecular biologists.
See also:
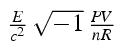 molecular information theory:
Information theory
applied to molecular patterns and states.
The more general term is
Biological
Information
Theory
=
BIT,
coined by
John Garavelli.
For a review see the
nano2
paper.
Google search for "molecular information theory".
molecular machine: The definition
given in
Channel
Capacity of Molecular Machines is:
molecular information theory:
Information theory
applied to molecular patterns and states.
The more general term is
Biological
Information
Theory
=
BIT,
coined by
John Garavelli.
For a review see the
nano2
paper.
Google search for "molecular information theory".
molecular machine: The definition
given in
Channel
Capacity of Molecular Machines is:
- A molecular machine is a single macromolecule or
macromolecular complex.
- A molecular machine performs a specific function for a living system.
- A molecular machine is usually primed by an energy source.
- A molecular machine dissipates energy as it does something specific.
- A molecular machine `gains'
information
by selecting between two or more
after states.
- Molecular machines are isothermal engines.
See:
molecular machine capacity:
The maximum
information,
in
bits
per
molecular operation
that a
molecular machine
can handle.
When translated into molecular biology, Shannon's
channel capacity theorem
states that
By increasing the number of independently moving parts
that can interact cooperatively to make decisions,
a molecular machine can reduce the error frequency
(rate of incorrect choices)
to whatever arbitrarily low level is required
for survival of the organism,
even when the machine operates near its capacity
and dissipates small amounts of power.
(quoted from page 112 of
T. D. Schneider, J. Theor. Biol., 83-123:, 112, 1991.)
This theorem explains the precision found
in molecular biology, such as the
ability of the restriction enzyme EcoRI
to recognize 5' GAATTC 3' while ignoring all other sites.
See the related
channel capacity.
The derivation is in
T. D. Schneider,
Theory of Molecular Machines. I. Channel Capacity of Molecular Machines. J.
Theor. Biol., 148:, 83-123, 1991.
molecular machine operation:
The thermodynamic process in which a
molecular machine
changes from the high energy
before state
to a
low energy
after state.
There are four standard examples:
-
Before
DNA hybridization the complementary strands
have a high relative potential energy;
after
hybridization the molecules are non-covalently
bound and in a lower energy state.
- The restriction enzyme
EcoRI selects 5' GAATTC 3' from all possible
DNA duplex hexamers. The operation is the transition from being
anywhere on the DNA to being at a GAATTC site.
- The molecular machine operation for rhodopsin,
the light sensitive pigment in the eye,
is the transition from having absorbed
a photon to having either changed configuration
(in which case one sees a flash of light)
or failed to change configuration.
- The molecular machine operation for actomyosin,
the actin and myosin components of muscle,
is the transition from having hydrolyzed an ATP
to having either changed configuration
(in which the molecules have moved one step
relative to each other)
or failed to change configuration.
motif:
See
pattern.
mutation:
a nucleic-acid sequence change that affects biological function,
for example by changing the
information content
of a
binding site.
A simple example is a
primary splice site mutation.
Delila instructions
can be used to create mutations, and
sequence walkers
can be used to distinguish mutations from polymorphisms.
Interestingly, a `mutation' depends on the function that one is
considering. For example, one could have two overlapping binding sites. A
sequence change can blow one away and leave the other one untouched (ie the
Ri
doesn't change). An interesting case of
a cryptic splice acceptor next to a normal acceptor
demonstrates how a single base change can have opposite effects on two splice
sites.
Another lovely example is the
ABCR mutation.
See also:
polymorphism,
leaky_mutation
and
a discussion on mutations and polymorphisms.
nanotechnology:
Technology on the nanometer scale.
The original definition is technology that is built
from single atoms and which depends on individual atoms
for function. An example is an enzyme. If you mutate the
enzyme's gene, the modified enzyme may or may not function.
In contrast, if you remove a few atoms from a hammer, it still
will work just as well. This is an important distinction that
has generally been lost as the hype about
nanotechnology
and it is used as a buzz word for 'small'
instead of a distinctly different technology.
Fortunately real nanotechnologies are in the works.
See:
nat:
Natural units for information or uncertainty are given in nats or nits.
See nit for more.
negentropy:
Poor Terminology!
In his book
"What is life?"
Erwin Schrödinger said that
"What an organism feeds upon is negative entropy."
The term negentropy was defined by Brillouin
(L. Brillouin,
Science and Information Theory,
second,
Academic Press, Inc.,
New York,
1962,
page 116)
as `negative entropy', N = -S.
Supposedly living creatures feed on `negentropy' from the sun.
However it is impossible for entropy to be negative, so `negentropy' is
always a negative quantity.
The easiest way to see this is to consider the statistical-mechanics
(Boltzmann) form of the
entropy
equation:
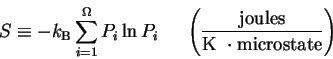
where kb is Boltzmann's constant,
 is the number of microstates of the system
and
Pi
is the probability of microstate i.
Unless one wishes to consider imaginary probabilities (!)
it can be proven that S is positive or zero.
Rather than saying `negentropy' or `negative entropy',
it is more clear to note that when a system
dissipates energy to its surroundings, its entropy decreases.
So it is better to refer to
-delta S (a negative change in entropy).
Recommendation:
replace this concept with
`decrease in entropy'.
is the number of microstates of the system
and
Pi
is the probability of microstate i.
Unless one wishes to consider imaginary probabilities (!)
it can be proven that S is positive or zero.
Rather than saying `negentropy' or `negative entropy',
it is more clear to note that when a system
dissipates energy to its surroundings, its entropy decreases.
So it is better to refer to
-delta S (a negative change in entropy).
Recommendation:
replace this concept with
`decrease in entropy'.
The term `feeding on negentropy' is misleading because
organisms eat physical matter (of course) that supplies them with
energy. The energy is used to put molecules into the
before state (H(X))
from which they THEN can make selections thereby gaining
information
by the molecule dropping to one of several possible
lower energy
after states (H(X|Y)).
The potential energy in a sugar molecule and then ATP
isn't directed initially to any particular choice and so isn't
associated with any information process until it is used for one.
The energy drop and the ultimate usefulness of energy comes
only from it being spread out - to increase the entropy of
the surroundings.
Examples:
-
In
"Maxwell's demon: Slamming the door"
(Nature 417: 903)
John Maddox
says
"Maxwell's demon ...
must be a device for creating negative entropy".
The Demon is required to create decreases in entropy, not
the impossible `negentropy'.
(Note: On 2002 July 6 Nature rejected a correspondence letter to point out
this error.)
nit:
Natural units for information or uncertainty are given in nits.
If there are M
messages,
then ln(M) nits are required to select one of them,
where ln is the natural logarithm with base e
(=2.71828...).
Natural units are used in thermodynamics where
they simplify the mathematics.
However nits are awkward to use
because results are almost never integers.
In contrast, the bit unit is easy to use because
many results are integer (e.g. log2 32 = 5)
and these are easy to memorize.
Using
the relationship
ln x / ln 2 = log2 x
allows one to present all results in bits.
See also:
- The appendix in the
primer on
information theory
gives a table of powers of two that is useful to memorize.
- bit
- nat is an alternative name for nit.
A little history is reported by David Dowe 2006 May 12:
In Boulton and Wallace (1970), the term "nit" is used.
It appears that J. Rissanen did not introduce the term "nat" before
1978.
I discuss this
very briefly on p271 (sec. 11.4.1) of Comley and Dowe (MIT Press, 2005).
Alan Turing (1912-1954) used the term "natural ban" for the same concept.
See his publications,
Comley and Dowe (2005)
page 271.
noise:
A physical process that interferes with transmission of a
message.
Shannon pointed out that the worst kind of noise has a Gaussian
distribution
Shannon1949.
Since
thermal noise
is always present in practical systems,
received messages will always have some probability
of having
errors.
parameter file:
Many
Delila
programs have parameter
files.
These are always simple text files, which is a robust
method that will work on any computer system.
Details on how to create the parameter file are always given on the
manual page for the program.
It is usually easiest to start from an example
(also given on the manual page) and modify it.
Parameters are given on individual text lines.
If the entire line is not a parameter,
then any text
after the parameter is ignored and serves as a comment.
For example,
the program
alist
is controled by a file
`alistp', which stands for alist-parameters.
Some parameter files now indicate the version number
of the program that they work with, and some programs
are now able to use this to upgrade the parameter file
automatically.
See also the
shell program.
parity bit:
A parity bit determines a
code
in which one data
bit
is set to either 0 or 1 so as to always
make a transmitted binary word contain an even or odd number of 1s.
The receiver can then count the number of 1's
to determine if there was a single error.
This code can only be used to detect an odd number of errors but
cannot be used to correct any error.
Unfortunately for molecular biologists,
the now-universal method for coding characters,
7 bit ASCII words,
assigns to the symbols for the nucleotide bases
A, C and G
only a one bit difference between A and C
and a one bit difference between C and G:
A: 1018 = 10000012
C: 1038 = 10000112
G: 1078 = 10001112
T: 1248 = 10101002
For example,
this choice could cause errors
during transmission of DNA sequences to the
international sequence repository,
GenBank.
If we add a parity bit on the front to make
an even parity code
(one
byte
long),
the situation is improved and more
resistant to
noise
because a single error will be detected when the number of 1s is odd:
A: 1018 = 010000012
C: 3038 = 110000112
G: 1078 = 010001112
T: 3248 = 110101002
Pascal's Triangle:
A triangle of numbers
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
in which each successive row is determined by
adding the two numbers to the upper left and right of a number.
The resulting distribution is a binomial distribution and in
the limit of infinite rows, it approaches a Gaussian distribution.
As pointed out by
Edward Tarte,
each number represents the number of ways that one can reach
that point in the triangle.
The concept of `ways' is, of course, the basis of the
Second Law of Thermodynamics.
It also shows that the Gaussian distribution is the `worst'
kind of noise,
as Shannon pointed out in 1949,
since all paths are taken without discrimination.
See also:
pattern:
see
sequence_pattern
John R. Pierce: An engineer at Bell Labs in the 1940s who
wrote an excellent introductory book about information theory:
An
Introduction to Information Theory:
Symbols, Signals and Noise.
Though one would think it is out of date, it is still more clear
and yet complete than anything else I have seen.
He gave a wonderful talk at Bell Labs in December, 1951 entitled
CREATIVE
THINKING.
pitfall:
An intellectual error that traps a researcher, perhaps forever.
See the
pitfalls
web page for examples.
See also
blind alley
and
La Brea tar pits.
plörk, plurk:
[Pronunciation: plûrk as in `work' and `urge'.
Function: noun.
Etymology: English from play and work, coined by TD Schneider;
umlaut suggested by HA Schneider to ensure correct pronunciation.
The umlaut is also a reference to their Austrian heritage.
Alternative spelling suggested by LR Schneider Engle: plurk.
Date: 2000. Earlier independent origin in 1997
by Teri-E Belf in the book
Simply Live It Up: Brief Solutions]
Play-work.
Plörk is what scientists do.
It is the enthusiastic, energetic application of oneself to the
task at hand as a child excitedly plays;
it is the intense arduous, meticulous work of an artist
on their life-long masterpiece; it is joyful work.
2004 May 13:
The 1997 book
Simply Live It Up: Brief Solutions
by Teri-E Belf
introduces the term plurk in three chapters, starting on page 143.
polymorphism:
a DNA sequence change that does not affect biological function,
or affects it non-lethally.
Delila instructions
can be used to create polymorphisms, and
sequence walkers
can be used to distinguish polymorphisms from mutations.
See also: mutation
and
a discussion on mutations and polymorphisms.
position: a number defining where one is
relative
to the
zero coordinate
of a
binding site.
probability:
The number of occurances of an event
in the entire population.
See also:
frequency.
qubit:
A "quantum bit" is a device that can store not only two states,
as a classical
bit,
but
also, as in quantum mechanics, a superposition of two states.
An example would be an electron in a magnetic field being either
'up', 'down' or a superposition of these states.
Supposedly one could have an electron 'entangled' with another
electron and do computation using them.
I am not an expert in this field,
but it is appropriate to at least mention it.
This glossary is for Molecular Information Theory,
not quantum information theory.
The strong distinction between these two topics is that for quantum
computers people want to avoid 'decoherence'
because this destroys quantum computations. That is, they wish to
avoid thermal noise. In the long run, this is basically impossible,
but they might be able to do it for a long enough time to sneak a
useful computation in.
(It is impossible because of the third law of thermodynamics
which says one cannot extract all the heat from a system to get
it to absolute zero. However one might extract enough that
there are only a few phonons of sound bouncing around.)
In contrast,
molecules in living things are totally
bombarded by thermal noise (a "thermal maelstrom",
ccmm) in
which decoherence would happen quickly.
So in the field of molecular information theory
and biology in general
on this planet, which is at 300K,
it seems unlikely that one will find qubits in biological systems.
See also:
 quincunx:
a device invented by Galton that demonstrates how the
Gaussian distribution
is generated.
The device, shown to the right
(source:
Wikipedia),
has balls starting from a single point
that traverse through a field of pins and are collected
into a series of slots at the bottom.
The path of each ball has two reasonably random possibilities
at each pin, so the final position of the balls forms
a binomial distribution, which is a good approximation to
a Gaussian distribution when there are many slots for collecting the balls.
When multiple Gaussian distributions are joined at right angles,
they form a sphere.
quincunx:
a device invented by Galton that demonstrates how the
Gaussian distribution
is generated.
The device, shown to the right
(source:
Wikipedia),
has balls starting from a single point
that traverse through a field of pins and are collected
into a series of slots at the bottom.
The path of each ball has two reasonably random possibilities
at each pin, so the final position of the balls forms
a binomial distribution, which is a good approximation to
a Gaussian distribution when there are many slots for collecting the balls.
When multiple Gaussian distributions are joined at right angles,
they form a sphere.
 See also:
range: The region of positions ("from" to "to") that covers the site.
The range can be chosen as the region which has significant
sequence conservation above the fluctuation of conservation caused
by
small samples of sequence.
Generally this can be done by looking
at a
sequence logo.
See
R. M. Stephens and T. D. Schneider, Features of
spliceosome evolution and function inferred from an
analysis of the information at human splice sites, J.
Mol. Biol., 228: 1124-1136, 1992.
recognizer: A general term for a macromolecule that recognizes
a specific pattern on a nucleic acid.
This includes
proteins such as transcription factors and protein/RNA complexes such
as ribosomes and spliceosomes.
See:
binding site.
relative coordinate: A number (usually integer)
that describes a specific position on a nucleic acid or protein sequence,
as an offset from an
absolute coordinate.
An example of using relative coordinates in
Delila instructions is:
"get from 3 -2 to 3 +2;" The numerals
-2
and
+2
are coordinates relative to the absolute coordinate
+3.
Rfrequency: The amount of
information
needed to find a set of binding sites
out of all the possible sites in the genome.
If the genome has G possible binding sites and
γ binding sites, then
Rfrequency =
Hbefore
-
Hafter
=
log2G
-
log2γ
=
log2G/γ
=
-log2γ/G
bits per site.
Note that
γ/G is the frequency of the sites in the genome.
Rfrequency predicts the expected information in a binding site,
Rsequence.
See also:
range: The region of positions ("from" to "to") that covers the site.
The range can be chosen as the region which has significant
sequence conservation above the fluctuation of conservation caused
by
small samples of sequence.
Generally this can be done by looking
at a
sequence logo.
See
R. M. Stephens and T. D. Schneider, Features of
spliceosome evolution and function inferred from an
analysis of the information at human splice sites, J.
Mol. Biol., 228: 1124-1136, 1992.
recognizer: A general term for a macromolecule that recognizes
a specific pattern on a nucleic acid.
This includes
proteins such as transcription factors and protein/RNA complexes such
as ribosomes and spliceosomes.
See:
binding site.
relative coordinate: A number (usually integer)
that describes a specific position on a nucleic acid or protein sequence,
as an offset from an
absolute coordinate.
An example of using relative coordinates in
Delila instructions is:
"get from 3 -2 to 3 +2;" The numerals
-2
and
+2
are coordinates relative to the absolute coordinate
+3.
Rfrequency: The amount of
information
needed to find a set of binding sites
out of all the possible sites in the genome.
If the genome has G possible binding sites and
γ binding sites, then
Rfrequency =
Hbefore
-
Hafter
=
log2G
-
log2γ
=
log2G/γ
=
-log2γ/G
bits per site.
Note that
γ/G is the frequency of the sites in the genome.
Rfrequency predicts the expected information in a binding site,
Rsequence.
Why is G not necessarily the genome size? G is the
number of distinct places that a protein (for example) can bind to the
genome. So the asymmetric bacteriophage T7 RNA polymerase can bind in
two ways to each base pair. For example, the E. coli genome is
a 4.7x106bp circle. That means that the polymerase could
bind in G = 2x4.7x106 ways. In thermodynamic terms, G is
the number of microstates possible (in the before state).
For a ribosome, the genome is pretty much only transcribed once
and not the complement (which would cause trouble because the
complements would bind together blocking translation among other
effects). So there are only G = 4.7x106 ways in that case.
If a protein has dimeric symmetry (e.g. LacI, TrpR, LexA,
etc) then it has two ways to bind, and G = 2x4.7x106. But
there are also twice as many ways to bind at each binding sites (two
at each base pair) so these extra factors of 2 cancel in the
computation of Rf.
See also
Schneider1986.
Ri:
Short hand notation for
individual information.
Following
Claude Shannon,
the `R' stands for a `rate of
information,
transmission'.
For molecular biologists this is usually
bits
per base or bits per amino acid.
The `i' stands for `individual'.
Ribl
or
Ri(b,l):
a
weight matrix
constructed using
individual information
theory that is a model
for a
binding site.
-
The `R' stands for `rate of information transmission' (following
Shannon) in bits per site.
-
The `i' stands for `individual' (it is not a subscript).
-
The `b' stands for `base', the nucleotide a, c, g or t.
-
The `l' stands for `position' in the site, which covers
the
range defined for the site.
Rsequence: The total amount of
information
conserved in a
binding site,
represented as the area under the
sequence logo.
Rsequence is computed as
the recognizer's
uncertainty
before binding
minus its uncertainty after binding.
The uncertainty before binding could be
2 bits per base
if you adhere to the philosophy
that the recognizer cannot account for base composition
when it is not bound.
Alternatively,
The uncertainty before binding could be
the uncertainty computed from the genome
(for DNA recognizers)
or the parts of the genome that
are available to the recognizer
(for RNA recognizers).
Using the genomic uncertainty will remove apparent background
information, but this may not be the right thing to do
since that might actually be information from binding proteins.
The uncertainty after binding is computed
from an
aligned
set of binding sites.
It is not appropriate to compute the information in binding
sites using the likelyhood function,
as Gary Stormo does,
because
then you won't get bits since you can
get results that claim to
have more than 2 bits of information for positions that
are entirely one base.
Of course that violates the definition of information from Shannon.
It is important to
correct for small numbers of sequences.
See also
information,
uncertainty,
Rfrequency,
recognizer,
Schneider1986.
science:
Score:
Poor Terminology!
Many methods in "bioinformatics" give results as "scores".
These ratings can be multiplied by an arbitrary constant and one
still can compare them.
In contrast,
information
is measured in
bits,
and this cannot
be multiplied by an arbitrary constant and still retain the same
units of measure.
Scores cannot be compared between different binding sites,
whereas it is reasonable to compare bits.
For example, it is interesting that
donor splice sites
do not have the same information as
acceptor splice sites
(Stephens and Schneider J. Mol. Biol., 228: 1124-1136, 1992).
Bits are not 'scores'. Would you call measured
binding energies scores? No? Then notice that energy is closely
related by an inequality to information, see:
T. D. Schneider
Theory of Molecular Machines.
II. Energy Dissipation from Molecular Machines
J. Theor. Biol.,
148 (1):
125-137,
1991.
That's a version of the
Second Law of Thermodynamics.
Bits are on an absolute scale that is directly related to the
physical universe.
Also, scores generally are integers but bits are real numbers.
The distinction between scores and bits becomes critical when one
is interested in computing the efficiency of a molecular system.
Scores cannot be used, but bits can be compared to the energy
by using the second law as an ideal conversion factor.
See the discovery
70% efficiency of bistate molecular machines explained by information
theory, high dimensional geometry and evolutionary convergence.
See also sequence_conservation.
Second Law of Thermodynamics:
The principle that
the disorder of an isolated system (entropy)
increases to a maximum. The Second Law appears in many surprisingly distinct
forms.
Transformations between these forms were described by
Ed T. Jaynes
(http://bayes.wustl.edu/)
in a beautiful paper
(Jaynes, E. T., 1988, ``The Evolution of Carnot's Principle'' in
Maximum-Entropy and Bayesian Methods in Science and Engineering, 1, G. J.
Erickson and C. R. Smith (eds.), Kluwer, Dordrecht, p. 267;
http://bayes.wustl.edu/etj/node1.html#carnot number 65,
http://bayes.wustl.edu/etj/articles/ccarnot.pdf,
http://bayes.wustl.edu/etj/articles/ccarnot.ps.gz postscript
(56Kb) file.)
The second law has many forms, and they do allow increase or decrease
of entropy. In particular, dS >= dQ/T, the entropy change (increase)
is always equal or greater than the heat input at some temperature T.
Multiply both sides by -1 to get -dS <= -dQ/T, the entropy decrease is
less than the heat dissipated (-dQ) at T. A snowflake is an example:
heat leaves the region and the snowflake crystalizes into patterns.
The relevant form for
molecular information theory
is
Emin = kB T ln(2) = -q/R (joules per bit),
where:
kB is Boltzmann's constant,
T is the absolute temperature,
ln(2) is a constant that converts to
bits,
-q is the heat dissipated away from the molecular machine,
and
R is the
information
gained by the molecular machine.
This form is derived in
T. D. Schneider,
Theory of Molecular Machines. II. Energy Dissipation from Molecular Machines
J. Theor. Biol., 148: 125-137, 1991.
Supposedly
Maxwell's demon
violates
the Second Law,
but if we approach the question from the viewpoint of
modern molecular biology,
the puzzles go away, as described in:
T. D. Schneider,
Sequence Logos, Machine/Channel Capacity, Maxwell's Demon, and Molecular
Computers: a Review of the Theory of Molecular Machines Nanotechnology, 5,
1-18, 1994.
http://secondlaw.oxy.edu
is a light-hearted introduction to the "Mother of all Murphy's Laws":

It clarifies an issue that is often incorrectly presented in
discussions about entropy.
See the other references by Frank Lambert below.
See also:
- An Equation for the Second Law of Thermodynamics
- Information
Is Not Entropy, Information Is Not Uncertainty!
- Rock Candy: An Example of
the Second Law of Thermodynamics
- Frank Lambert works at
http://entropysite.oxy.edu:
- ENTROPY and the Second Law of Thermodynamics!
- Disorder -- A Cracked Crutch for Supporting Entropy Discussions
Journal of Chemical Education, February 2002 Vol. 79 No. 2 p. 187.
- Entropy Is Simple, Qualitatively
Journal of Chemical Education, October 2002 Vol. 79 No. 10 p. 1241.
-
Lambert, Frank L. Shuffled Cards, Messy
Desks, and Disorderly Dorm Rooms - Examples of
Entropy Increase? Nonsense! J. Chem. Educ. 1999,
76: 1385-1387.
- F. L. Lambert, The Conceptual Meaning of Thermodynamic Entropy in
the, 21st Century, International Research Journal
of Pure & Applied, Chemistry, 1, 65-68
2011.
-
MIT course: Aeronautics and Astronautics, Thermal Energy, Fall 2002
16.050 Thermal Energy
-
Basic Thermodynamics according to cartooninst Sidney Harris
-
Thermodynamics for Two, Please
by R. J. Riggins, darrwin@aol.com.
(my archival copy:
Riggins)
- Sodaplay demonstration of entropic rubber
- The book "The Second Law" by P. W. Atkins gives an excellent
intuitive explanation for entropy and how it works in various systems.
- google: Flanders and Swann song about entropy
youtube: Flanders & Swann - 'First And Second Law'
Published on Feb 14, 2013
"From the stage performance 'At The Drop Of Another Hat' in 1964"
another
lyrics
Sequence conservation (conservation):
Surprisingly,
the degree of biological sequence conservation is neatly given
in
bits of information.
One can envision that eventually all forms of biological conservation
could be measured this way.
 sequence logo: A graphic representation of an
aligned set of sequences,
including DNA and RNA
binding sites
or protein sequences invented by Tom Schneider (owner of this website)
and Mike Stephens.
A logo displays the frequencies of bases or amino acids at each position,
as the relative heights of letters,
along with the degree of
sequence conservation
as the total height of a stack of letters,
measured in bits of
information.
Subtle frequencies are
not lost in the final product as they would be in a
consensus sequence.
The vertical scale is in bits, with a maximum of 2 bits possible at each
position for DNA or RNA (with 4 bases,
log24 = 2 bits per base)
and log220 = 4.3 bits per amino acid for proteins.
Note that sequence logos are an average
picture of a set of binding sites
(which is why logos can have several letters in each stack)
while
sequence walkers
are the individuals that make up that average
(which is why walkers have only one letter per
position).
sequence pattern:
A sequence pattern is defined by
the nucleotide sequences of a
set of aligned binding sites
or by a common protein structure.
In contrast,
consensus sequences,
sequence logos
and
sequence walkers
are only models of the patterns found experimentally or in nature.
Models do not capture everything in nature. For example, there
might be correlations between two different
positions in a binding site.
A more
sophisticated model
might capture these but still not
capture three-way correlations.
It is impossible to make the more detailed model if there is not enough
data.
(In a more zen-like mood, we should note that everything we
sense and observe is a model ...)
See also:
sequence logo: A graphic representation of an
aligned set of sequences,
including DNA and RNA
binding sites
or protein sequences invented by Tom Schneider (owner of this website)
and Mike Stephens.
A logo displays the frequencies of bases or amino acids at each position,
as the relative heights of letters,
along with the degree of
sequence conservation
as the total height of a stack of letters,
measured in bits of
information.
Subtle frequencies are
not lost in the final product as they would be in a
consensus sequence.
The vertical scale is in bits, with a maximum of 2 bits possible at each
position for DNA or RNA (with 4 bases,
log24 = 2 bits per base)
and log220 = 4.3 bits per amino acid for proteins.
Note that sequence logos are an average
picture of a set of binding sites
(which is why logos can have several letters in each stack)
while
sequence walkers
are the individuals that make up that average
(which is why walkers have only one letter per
position).
sequence pattern:
A sequence pattern is defined by
the nucleotide sequences of a
set of aligned binding sites
or by a common protein structure.
In contrast,
consensus sequences,
sequence logos
and
sequence walkers
are only models of the patterns found experimentally or in nature.
Models do not capture everything in nature. For example, there
might be correlations between two different
positions in a binding site.
A more
sophisticated model
might capture these but still not
capture three-way correlations.
It is impossible to make the more detailed model if there is not enough
data.
(In a more zen-like mood, we should note that everything we
sense and observe is a model ...)
See also:
- Correlations in splicing
- RNA Structure Logo
- Consensus Sequence Zen
T. D. Schneider,
Applied Bioinformatics,
1,
111-119,
2002,
is a paper that discusses this topic.
-
D. Purves, R. B. Lotto, and S. Nundy.
Why we see what we do,
Amer. Sci., 90(3):236-243, May-June 2002.
 sequence walker: A graphic representation of a single
possible binding site,
with the height of letters indicating how bases match the
individual information
weight matrix
at each
position. Bases that have positive values in the
weight matrix
are shown
right-side up; bases that have negative values are shown upside down
and below the "horizon". As in a
sequence logo,
the vertical scale is in bits; the maximum is 2 bits and the minimum is
negative infinity. Bases that do not appear in the set of aligned sequences
are shown negatively and in a black box. Bases that have negative values
lower than can fit in the space available have a purple box.
The
zero coordinate
is inside a rectangle which
(in this case)
runs from -3 to +2 bits in height.
If the background of the rectangle
is light green, the sequence has been evaluated as a binding site,
while if it is pink it is not a binding site.
sequence walker: A graphic representation of a single
possible binding site,
with the height of letters indicating how bases match the
individual information
weight matrix
at each
position. Bases that have positive values in the
weight matrix
are shown
right-side up; bases that have negative values are shown upside down
and below the "horizon". As in a
sequence logo,
the vertical scale is in bits; the maximum is 2 bits and the minimum is
negative infinity. Bases that do not appear in the set of aligned sequences
are shown negatively and in a black box. Bases that have negative values
lower than can fit in the space available have a purple box.
The
zero coordinate
is inside a rectangle which
(in this case)
runs from -3 to +2 bits in height.
If the background of the rectangle
is light green, the sequence has been evaluated as a binding site,
while if it is pink it is not a binding site.
 See the sequence walker paper page.
See the sequence walker paper page.
- Examples:
- An example of many sequence walkers
Fis Promoter Map
- The top figure to the right shows a sequence walker for a human
donor splice site.
- The larger figure has two sequence logos on top and five of the
individual sequences used to generate the logos on the bottom.
Sequence walkers are intimately entangled with sequence walkers.
-
Figure 4 of
Rogan.Faux.Schneider1998
shows sequence walkers for human
acceptor splice sites
at intron 3 of
the iduronidase synthetase gene
(IDS, L35485).
An A to G mutation
decreases the
information content of the
normal site while
simultaneously
increasing the information content of a cryptic site,
leading to a genetic disease.
The top sequence is normal
and the 12.7 bit acceptor at 5154 is used.
Note how the
zero position
of this walker is just upstream of the exon (dashed).
There is a strong cryptic site at
5153 that is presumably not normally used.
The mutation reverses the strengths of the acceptors,
leading to a frame shift and hence to a genetic disease.
-
ABCR Mutation G863A
- A beautiful example is the cluster of Fis sites (in pink and
red shades) that control the Fis gene itself:
Fis Promoter Map
- There are some examples in the
lister program documentation.
Lister is used to make walkers.
-
Original References:
- Servers:
-
For further information:
see the
web page on walkers
Claude E. Shannon (April 30, 1916 - February 24, 2001):
An engineer at Bell Labs in the 1940s who developed
information theory.
His most famous work is
A Mathematical Theory of Communication, published in 1948.
As a consequence of his work, we now have clear communication systems,
including long distance voice phone calls, CDs without static, and the internet.
Shannon was
known to
juggle and ride his unicycle in the halls of Bell Labs.
See also:
- Bell Labs Claude Shannon, Father of Information Theory, Dies at 84.
- Tribute To Shannon
by John S. Garavelli, Thomas D. Schneider and John L. Spouge.
- Tribute To Shannon
by Gerard Battail (with permission to publish on the web)
- Shannon Statue Dedications
- Historical description
- bit.
- information.
- uncertainty.
- channel capacity.
- Google Scholar: Claude E. Shannon
- Significant papers - online:
-
Shannon1948:
A Mathematical Theory of Communication,
C. E. Shannon,
Bell System Tech. J., 27
379-423, 623-656, 1948.
second part
-
Shannon1949:
Communication in the Presence of Noise,
C. E. Shannon,
Proc. IRE, 37, 10-21, 1949.
second link
- Movie:
The Bit Player
Trailer.
Website
Shannon Entropy:
Poor Terminology!
The story goes that
Shannon didn't know what to call his measure and so asked
the famous mathematician von Neumman. Von Neumann
said he should call it the entropy because nobody knows what that
is and so Shannon would have the advantage in every debate!
This has led to much confusion in the literature
because
entropy
has different units than
uncertainty.
It is the latter which is usually meant.
If one does not use correct units, one will not get correct
results.
Recommendation:
if you are making computations from symbols,
always use the term
uncertainty, with recommended units of
bits per symbol.
If you mean the entropy of a physical system, then
use the term
entropy, which has units of joules per kelvin
(energy per temperature).
See:
The story is paraphrased from
M. Tribus and E. C. McIrvine,
"Energy and Information",
Sci. Am.,
225,
(Note: the table of contents in this volume incorrectly lists this as volume 224),
3,
179-188,
September,
1971.
(PDF link) Here's the story:
What's in a name? In the case of Shannon's
measure the naming was not accidental.
In 1961 one of us (Tribus)
asked Shannon what he had thought
about when he had finally confirmed his
famous measure. Shannon replied: "My
greatest concern was what to call it. I
thought of calling it 'information,' but
the word was overly used, so I decided
to call it 'uncertainty.' When I discussed
it with John von Neumann, he had a better
idea. Von Neumann told me, 'You
should call it entropy, for two reasons.
In the first place your uncertainty function
has been used in statistical mechanics
under that name, so it already has a
name. In the second place, and more
important, no one knows what entropy
really is, so in a debate you will always
have the advantage.'
Shannon sphere:
A sphere in a high dimensional space which represents either
a single
message
of a communications system
(after sphere)
or the volume that contains all possible messages
(before sphere)
could be called a Shannon sphere, in honor of Claude
Shannon
who recognized its importance in
information_theory.
The radius of the smaller after spheres is determined
by the ambient thermal noise,
while that of the larger
before sphere is determined
by both the
thermal noise and the signal power
(signal-to-noise ratio),
measured at the receiver.
The logarithm of the number of
small spheres that can fit into the larger sphere
determines the
channel capacity
(See: Shannon1949).
The high-dimensional packing of the spheres
is the coding of the system.
There are two ways to understand how the spheres come to be.
Consider a digital message
consisting of independent voltage pulses.
The independent voltage values specify a point in a high dimensional space
since independence is represented by coordinate axes set at right
angles to each other. Thus three voltage pulses correspond to a point
in a 3 dimensional space and 100 pulses correspond to a point
in a 100 dimensional space.
The first `non-Cartesian' way to understand the spheres is to note that
thermal noise interferes with the initial
message during transmission of the information such that the received
point is dislocated from the initial point.
Since noisy distortion can be in any direction, the set of all possible
dislocations is a sphere.
The second `Cartesian' method is to note that the
sum of many small dislocations to
each pulse, caused by thermal noise, gives a Gaussian distribution
at the receiver.
The probability that a received pulse is disturbed a
distance x from the initial voltage is
of the form
p(x) ≈ e-x2.
Disturbance of a second pulse will have the same form,
p(y) ≈ e-y2.
Since these are independent,
the probability of both distortions
is multiplied:
p(x,y) = p(x) p(y).
Combining equations,
p(x,y) ≈ e-(x2 + y2)
= e-r2, where r is the radial
distance. If p(x,y) is a constant, the locus of all points enscribed
by r is a circle. With more pulses the same argument holds, giving
spheres in high dimensional space.
Shannon used this construction in his
channel capacity
theorem.
For a
molecular machine
containing n atoms there can be as many as
3n-6 independent components (degrees of freedom)
so there can be
3n-6 dimensions.
The velocity of these components corresponds to the voltage
in a communication system and they are disturbed by thermal
noise. Thus the state of a molecular machine can also
be described by a sphere in a high dimensional velocity space.
See also:
signal-to-noise ratio:
The ratio between the received signal power and the
noise
at the receiver of a communications system.
In molecular biology, the equivalent is the energy dissipated
divided by the thermal noise.
See
site: See binding site.
skew, genomic:
see genomic skew.
small sample correction:
a correction to the
Shannon
uncertainty
measure to account for the effects of small sample sizes.
See:
specificity:
Poor Terminology!
The term is often ill defined. It has been used to
refer to livers (tissue specificity), energy,
binding constants,
error rates,
binding patterns (like what a
sequence logo
shows)
and other mutually inconsistent concepts.
Recommendation:
use the appropriate precise term (energy, bits, information etc.) instead.
The point I will try to make today is that one of the bigger problems
I think a field like immunology has is really that we tend to use
words that instill the feeling of understanding things but in fact
only obfuscate things. And I just just pick one of these terms, um,
specificity, you know we measure antibody activities in an Eliza so we
stick something on plastic and hope the antibody sticks to the stuff
that sticks on plastic and then we say we have a signal and this is
important. Now when you measure most of these antibody qualities the
binding quality is in the order of ten to the minus five to ten to the
minus six molar. But when you then do measurements and assay
antiviral or antibacterial protective antibodies you find that the
avidities are in the order of ten to the minus nine molar. So a
thousand to ten thousand times away from the scale you usually use.
-- Rolf Zinkernagel, M.D., Ph.D., Zurich University and 1996 Nobel Laureate
in a talk at NIH, "Anti-Viral Immunity and Vaccines"
Wednesday, April 14, 2004.
(3 minutes 10 seconds into the talk.)
(search for Zinkernagel,
direct video link)
surprisal:
How surprised one would be by a single symbol in a stream of symbols.
It is computed
from the probability of the ith symbol,
Pi,
as
ui = - log2Pi.
For example, late at night, as I write this,
the phone rarely rings so the probability
of silence is close to 1 and the surprisal for silence is near zero.
(If the probability of silence is 99% then
usilence = - log20.99 = 0.01
bits per second, where the phone can ring only once per second.)
On the other hand, a ring is rare so the surprisal
for ringing is very high.
(For example,
if the probability of ringing is 1% per second then
uring = - log20.01 = 6.64
bits per second.)
The average of all surprisals over the entire signal
is the uncertainty.
(0.99 * 0.01 + 0.01 * 6.64 = 0.08
bits per second in this "phone"y example. ;-)
The term comes from Myron Tribus' book
"Thermostatics and Thermodynamics"
(D. van Nostrand Company, Inc.,
Princeton, N. J.,
1961).
symbol:
two or more discrete physical states of a physical system
associated with living beings. The states become separated from each
other during the co-evolution of the beings and the symbols.
Shannon's channel capacity theorem gurarantees that the states can be
distinguished sufficiently for the survival of the organisms.
See
symmetry:
See
binding site symmetry.
thermal noise:
Thermal noise is caused by the
random motion of molecules at any temperature
above absolute zero Kelvin.
Since the third law of thermodynamics prevents one from extracting
all heat from a physical system,
one cannot reach absolute zero and so cannot entirely
avoid thermal
noise.
In 1928 Nyquist worked out the thermodynamics of noise
in electrical systems and in a back-to-back paper
Johnson demonstrated that the theory was correct.
See:
- noise.
- H. Nyquist,
"Thermal agitation of electric charge in conductors",
Physical Review, 32, 110-113, 1928.
-
J. B. Johnson,
"Thermal agitation of electricity in conductors",
Physical Review,
32,
97-109,
1928.
-
Johnson-Nyquist noise at Wikipedia.
to: The 3' extent of the range of a binding site.
For example in a
Delila instruction
one might have
get from 50 -10 to
same +5; the range runs from -10 to +5.
tominology:
[Pronunciation: tom-in-ology,
Function: noun,
Etymology: coined by TD Schneider,
from the accidental combination of `Tom' and `terminology',
Date: 2002 August 26].
Tom's obscure terminology, such as the word
Rsequence,
plurk, etc.
Generally one should use the available terminology, but
one should not fear inventing
invent new terminology to describe new things.
uncertainty:
A logarithmic measure of the average number of
choices that a receiver
or a molecular machine has available.
The uncertainty is computed as:
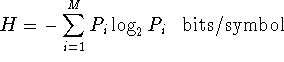
where Pi is the probability of the ith
symbol and M is the number of symbols.
Uncertainty is the average surprisal.
The
information is the difference between
the uncertainty before
and
the uncertainty after
symbol transmission.
See also:
walker:
See:
sequence walker.
weight matrix:
A two dimensional array of numbers that assigns to all possible
sequences a weight.
There are many methods for creating weight matrices:
- neural networks
(G. D. Stormo,
T. D. Schneider,
L. Gold
and A. Ehrenfeucht,
Use of the `Perceptron' algorithm to distinguish translational
initiation sites in E. coli,
Nucleic Acids Res.,
10,
2997-3011,
1982)
- solving linear equations
(G. D. Stormo,
T. D. Schneider
and L. Gold,
Quantitative analysis of the relationship between nucleotide
sequence and functional activity,
Nucleic Acids Res.,
14,
6661-6679,
1986;
D. Barrick,
K. Villanueba,
J. Childs,
R. Kalil,
T. D. Schneider,
C. E. Lawrence,
L. Gold,
and G. D. Stormo,
Quantitative Analysis of Ribosome Binding Sites in
E. coli.,
Nucleic Acids Res.,
22,
1287-1295,
1994)
-
information theory
by the method of
individual information.
zero coordinate (zero base, zero position):
The position by which
a set of
binding sites
is
aligned.
Not having a zero as part of your
coordinate system
is a
bad idea
 because it makes computations tricky.
On the positive side, having a zero coordinate allows one to precisely
define the location of a binding site or other feature.
In particular, it allows one to place a
sequence walker.
See also:
because it makes computations tricky.
On the positive side, having a zero coordinate allows one to precisely
define the location of a binding site or other feature.
In particular, it allows one to place a
sequence walker.
See also:
 Possible new terms to be added:
Possible new terms to be added:
- communications channel
- transmitter
- receiver
Do you have a suggestion?

|
Dictionary of Bioinformatics and Computational Biology,
Hancock, John M. / Zvelebil, Marketa J. (eds.).
(John Wiley & Sons, Inc.,
Hoboken, New Jersey,
ISBN 0-471-43622-4,
2004.)
I (Thomas D. Schneider) am one of the contributors.
Many of the terms in this Glossary are in the Dictionary,
and all of the terms in the Dictionary are in this Glossary.
new as of 2004 August 5.
|
Acknowledgments
I thank Brent Jewett,
Ryan Shultzaberger,
Ilya Lyakhov,
Jim Ellis,
Krishnamachari Annangarachari (Chari),
Danielle Needle,
Guido De Mey (qubit),
Bogdan S. Pecican
(symbol, choice, certainty, communication),
Mileidy Gonzalez (Rfrequency computation),
Colin Kline
(Ballarat, Victoria, Australia;
probability and frequency)
and
David Dowe
(Monash University; Clayton; Victoria 3168; Australia;
nat)
for useful questions, comments, corrections and suggestions.


Schneider Lab.
origin: 1999 April 15
updated:
version = 3.64 of glossary.html 2023 Jul 12

|
This is the bottom of the
glossary.
The blank lines above this point ensure that the last
entry or entries start at the top of the page.
If you have come here by using a pointer, then
something is wrong, since
there is no such definition.
Please report the
error to me.
I'll need to know where you are so please send me the current url.
If you are in frame mode, please use Show Only This Frame in your browser
to get the correct url.
I'll also need to know where you were
so please back up with your browser to determine that and send
me that url too.
Thanks.
Tom Schneider
|
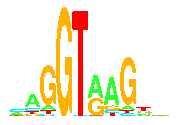
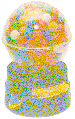
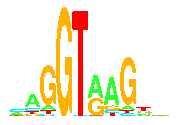
 as of 2011 Nov 12.
as of 2011 Nov 12.
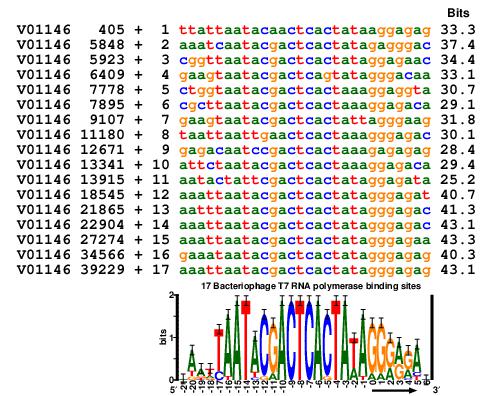




 See also:
See also:
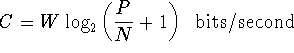
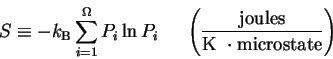
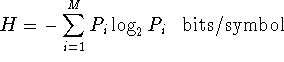
 gumball machine:
A model for the packing of
Shannon
spheres. Each gumball represents
one possible message or one possible molecular state
(an after sphere).
The radius of the gumball represents the
thermal noise.
The balls are all enclosed inside a larger sphere
(the before sphere)
whose radius
is determined from both the thermal noise and the power dissipated
at the receiver (or by the molecule) while it selects that state.
The way the spheres are packed relative to each other is the
coding.
See channel capacity
and molecular machine capacity.
gumball machine:
A model for the packing of
Shannon
spheres. Each gumball represents
one possible message or one possible molecular state
(an after sphere).
The radius of the gumball represents the
thermal noise.
The balls are all enclosed inside a larger sphere
(the before sphere)
whose radius
is determined from both the thermal noise and the power dissipated
at the receiver (or by the molecule) while it selects that state.
The way the spheres are packed relative to each other is the
coding.
See channel capacity
and molecular machine capacity.
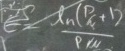

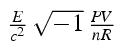
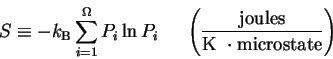
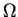 is the number of microstates of the system
and
Pi
is the probability of microstate i.
Unless one wishes to consider imaginary probabilities (!)
it can be proven that S is positive or zero.
Rather than saying `negentropy' or `negative entropy',
it is more clear to note that when a system
dissipates energy to its surroundings, its entropy decreases.
So it is better to refer to
-delta S (a negative change in entropy).
Recommendation:
replace this concept with
`decrease in entropy'.
is the number of microstates of the system
and
Pi
is the probability of microstate i.
Unless one wishes to consider imaginary probabilities (!)
it can be proven that S is positive or zero.
Rather than saying `negentropy' or `negative entropy',
it is more clear to note that when a system
dissipates energy to its surroundings, its entropy decreases.
So it is better to refer to
-delta S (a negative change in entropy).
Recommendation:
replace this concept with
`decrease in entropy'.

 See also:
See also:

 sequence logo: A graphic representation of an
aligned set of sequences,
including DNA and RNA
binding sites
or protein sequences invented by Tom Schneider (owner of this website)
and Mike Stephens.
A logo displays the frequencies of bases or amino acids at each position,
as the relative heights of letters,
along with the degree of
sequence conservation
as the total height of a stack of letters,
measured in bits of
information.
Subtle frequencies are
not lost in the final product as they would be in a
consensus sequence.
sequence logo: A graphic representation of an
aligned set of sequences,
including DNA and RNA
binding sites
or protein sequences invented by Tom Schneider (owner of this website)
and Mike Stephens.
A logo displays the frequencies of bases or amino acids at each position,
as the relative heights of letters,
along with the degree of
sequence conservation
as the total height of a stack of letters,
measured in bits of
information.
Subtle frequencies are
not lost in the final product as they would be in a
consensus sequence.
 as of 2011 Mar 10
as of 2011 Mar 10
 sequence walker: A graphic representation of a single
possible binding site,
with the height of letters indicating how bases match the
individual information
weight matrix
at each
position. Bases that have positive values in the
weight matrix
are shown
right-side up; bases that have negative values are shown upside down
and below the "horizon". As in a
sequence logo,
the vertical scale is in bits; the maximum is 2 bits and the minimum is
negative infinity. Bases that do not appear in the set of aligned sequences
are shown negatively and in a black box. Bases that have negative values
lower than can fit in the space available have a purple box.
The
zero coordinate
is inside a rectangle which
(in this case)
runs from -3 to +2 bits in height.
If the background of the rectangle
is light green, the sequence has been evaluated as a binding site,
while if it is pink it is not a binding site.
sequence walker: A graphic representation of a single
possible binding site,
with the height of letters indicating how bases match the
individual information
weight matrix
at each
position. Bases that have positive values in the
weight matrix
are shown
right-side up; bases that have negative values are shown upside down
and below the "horizon". As in a
sequence logo,
the vertical scale is in bits; the maximum is 2 bits and the minimum is
negative infinity. Bases that do not appear in the set of aligned sequences
are shown negatively and in a black box. Bases that have negative values
lower than can fit in the space available have a purple box.
The
zero coordinate
is inside a rectangle which
(in this case)
runs from -3 to +2 bits in height.
If the background of the rectangle
is light green, the sequence has been evaluated as a binding site,
while if it is pink it is not a binding site.
 See the sequence walker paper page.
See the sequence walker paper page.
 gumball machine
gumball machine
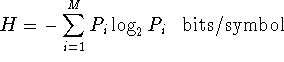
 because it makes computations tricky.
On the positive side, having a zero coordinate allows one to precisely
define the location of a binding site or other feature.
In particular, it allows one to place a
sequence walker.
See also:
because it makes computations tricky.
On the positive side, having a zero coordinate allows one to precisely
define the location of a binding site or other feature.
In particular, it allows one to place a
sequence walker.
See also:
 Possible new terms to be added:
Possible new terms to be added:



